误差反向传播
几个概念
对于某个具体的神经元
-
正向输入是前一层每一个神经元的正向输出与它相连的对应的权值乘积的求和
-
正向输出=f(正向输入),其中f为激活函数
-
反向输入是后一层每一个神经元的反向输出与它相连的对应的权值乘积的求和,
-
反向输出等于它的反向输入乘以激活函数在正向输入那一点的导数 (详细介绍请Google计算图)
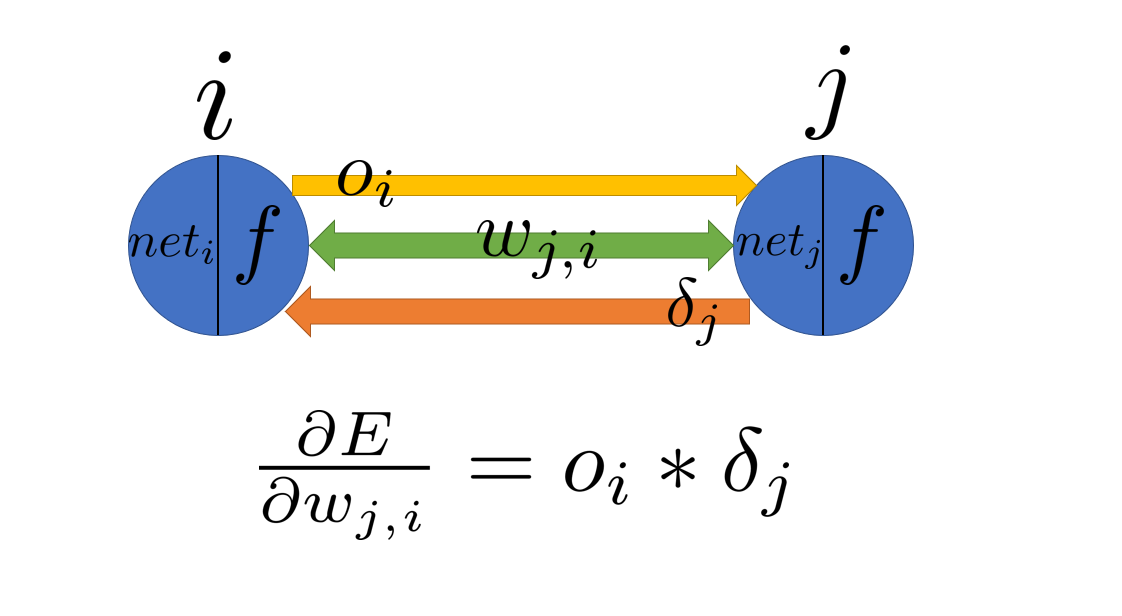
上述等式是链式法则的典型应用。
正向传播信号
神经元 $i$ 的正向输入是它的前一层神经元的正向输出和与它相连的权重的乘积的求和。
神经元 $i$ 的正向输入经过激活函数 $f$ 得到正向输出 $o_{i}$
$o_{i}$是神经元$i$的正向输出
$w_{j,i}$是神经元$i$和神经元$j$之间的权重
$\delta_{j}$是神经元$j$的反向输出
反向传播误差:所以反向传播,传播的是误差
神经元$j$的反向输入是它的后一层神经元的反向输出和与它相连的权重的乘积的求和。
神经元$j$的反向输入乘以它的激活函数在正向输入点的导数值得到神经元的反向输出$\delta_{j}$