1 人工智能三学派
- 行为主义 控制论
- 符号主义 专家系统
- 连接主义 神经元
2 CUDA cuDNN
-
CUDA: Compute Unified Device Architecture 相当于一个平台
C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.2
C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.2\lib\x64
加入环境变量,让系统能找到相应的动态库和程序
-
cuDNN: CUDA Deep Neural Network library 相当于一个插件 插到CUDA平台上, 用于深度神经网络的GPU加速库 所以下载好cuDNN之后,把其bin、include、lib目录下的文件复制到对应CUDA安装目录的bin、include、lib目录。(仔细想想为什么,还可以怎么做?)
3 激活函数
评判好坏:
-
梯度消失?
-
收敛速度?
-
运算速度?
-
Sigmoid
1
tf.nn.sigmoid(x)
-
容易造成梯度消失
-
输出非0均值,收敛慢
-
由于幂运算,训练时间长
-
-
tan h
1
tf.math.tanh(x)
-
容易造成梯度消失
-
输出0均值,收敛慢
-
由于幂运算,训练时间长
-
-
ReLU
1
tf.nn.relu(x)
优点:
-
解决了梯度消失的问题(正区间)
-
由于只需要判断与0的大小,运算速度快
-
收敛速度远快于前两个
缺点:
-
输入非0均值,收敛慢
-
Dead ReLU问题,送入激活函数的值小于0时,某些神经元永远不被激活,导致相应的参数永远不被更新? (Solver:设置更小的学习率,减少参数分布的巨大变化)
-
-
Leak ReLU
1
tf.nn.leaky_relu(x)
-
拥有ReLU的所有优点
-
实际中不一定比ReLU好
-
建议:
-
首选ReLU
-
学习率设置较小值
-
特征标准化 均值为0,标准差为1的正态分布
-
初始参数中心化,均值为0,标准差为$sqrt(2/当前层输入特征的个数)$的正态分布
4 欠拟合 过拟合 正则化
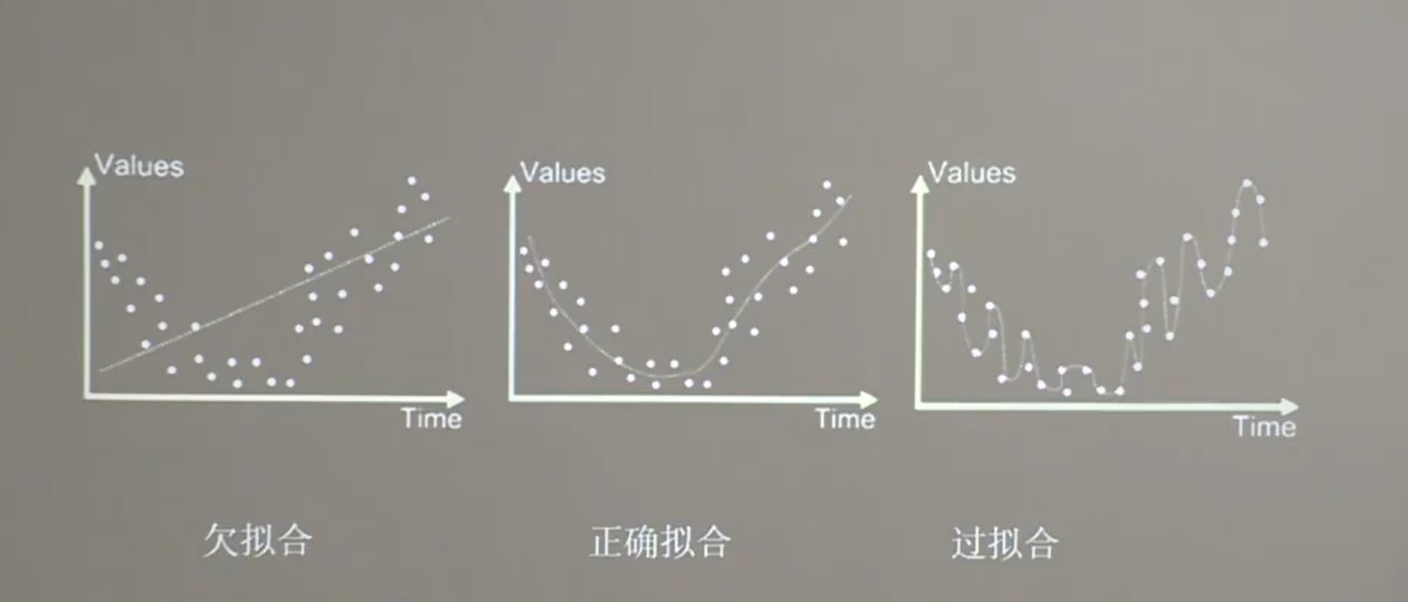
-
欠拟合
- 增加输入特征项
- 增加网络参数
- 减少正则化参数
-
过拟合
- 数据清洗,减少噪声
- 增大训练集
- 采用正则化
- 增大正则化参数

文件dot.csv内容如下:
1 | x1,x2,y_c |
-
未加入正则化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])
x_train = np.vstack(x_data).reshape(-1,2)
y_train = np.vstack(y_data).reshape(-1,1)
Y_c = [['red' if y else 'blue'] for y in y_train]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)
# from_tensor_slices函数切分传入的张量的第一个维度,生成相应的数据集,使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
# 生成神经网络的参数,输入层为2个神经元,隐藏层为11个神经元,1层隐藏层,输出层为1个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
lr = 0.01 # 学习率
epoch = 400 # 循环轮数
# 训练部分
for epoch in range(epoch):
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape: # 记录梯度信息
h1 = tf.matmul(x_train, w1) + b1 # 记录神经网络乘加运算
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss = tf.reduce_mean(tf.square(y_train - y))
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 实现梯度更新
# w1 = w1 - lr * w1_grad tape.gradient是自动求导结果与[w1, b1, w2, b2] 索引为0,1,2,3
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
# 每20个epoch,打印loss信息
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成间隔数值点
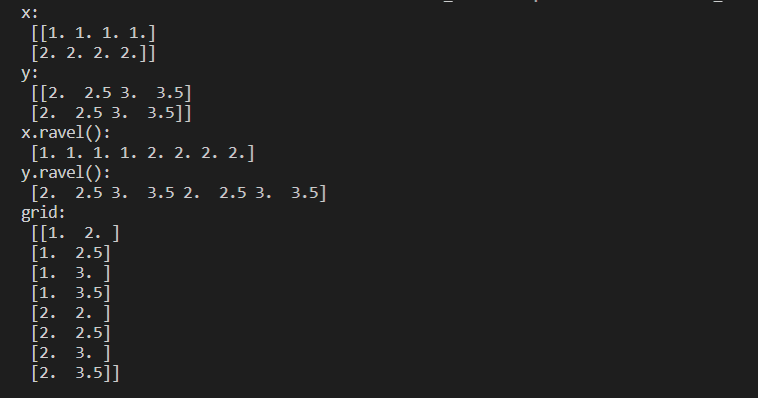
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx , yy拉直,并合并配对为二维张量,生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络,进行预测,probs为输出
probs = []
for x_test in grid:
# 使用训练好的参数进行预测
h1 = tf.matmul([x_test], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2 # y为预测结果
probs.append(y)
# 取第0列给x1,取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c)) #squeeze去掉纬度是1的纬度,相当于去掉[['red'],[''blue]],内层括号变为['red','blue']
# 把坐标xx yy和对应的值probs放入contour<[‘kɑntʊr]>函数,给probs值为0.5的所有点上色 plt点show后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()
# 读入红蓝点,画出分割线,不包含正则化
# 不清楚的数据,建议print出来查看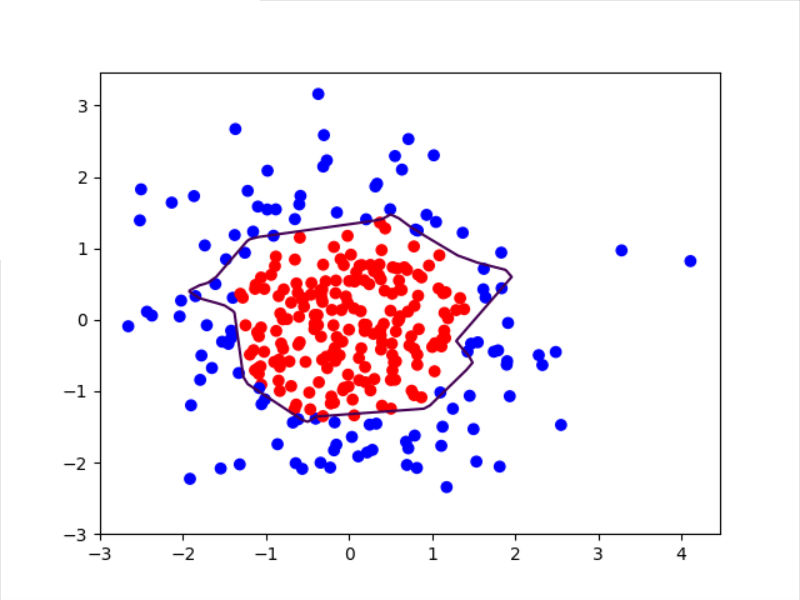
-
加入正则化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101# 导入所需模块
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据/标签 生成x_train y_train
df = pd.read_csv('dot.csv')
x_data = np.array(df[['x1', 'x2']])
y_data = np.array(df['y_c'])
x_train = x_data
y_train = y_data.reshape(-1, 1)
Y_c = [['red' if y else 'blue'] for y in y_train]
# 转换x的数据类型,否则后面矩阵相乘时会因数据类型问题报错
x_train = tf.cast(x_train, tf.float32)
y_train = tf.cast(y_train, tf.float32)
# from_tensor_slices函数切分传入的张量的第一个维度,生成相应的数据集,使输入特征和标签值一一对应
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
# 生成神经网络的参数,输入层为4个神经元,隐藏层为32个神经元,2层隐藏层,输出层为3个神经元
# 用tf.Variable()保证参数可训练
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
lr = 0.01 # 学习率为
epoch = 400 # 循环轮数
# 训练部分
for epoch in range(epoch):
for step, (x_train, y_train) in enumerate(train_db):
with tf.GradientTape() as tape: # 记录梯度信息
h1 = tf.matmul(x_train, w1) + b1 # 记录神经网络乘加运算
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
# 采用均方误差损失函数mse = mean(sum(y-out)^2)
loss_mse = tf.reduce_mean(tf.square(y_train - y))
# 添加l2正则化
loss_regularization = []
# tf.nn.l2_loss(w)=sum(w ** 2) / 2
loss_regularization.append(tf.nn.l2_loss(w1))
loss_regularization.append(tf.nn.l2_loss(w2))
# 求和
# 例:x=tf.constant(([1,1,1],[1,1,1]))
# tf.reduce_sum(x)
# >>>6
# loss_regularization = tf.reduce_sum(tf.stack(loss_regularization))
loss_regularization = tf.reduce_sum(loss_regularization)
loss = loss_mse + 0.03 * loss_regularization # REGULARIZER = 0.03
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 实现梯度更新
# w1 = w1 - lr * w1_grad
w1.assign_sub(lr * grads[0])image-20210512233454999
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
# 每200个epoch,打印loss信息
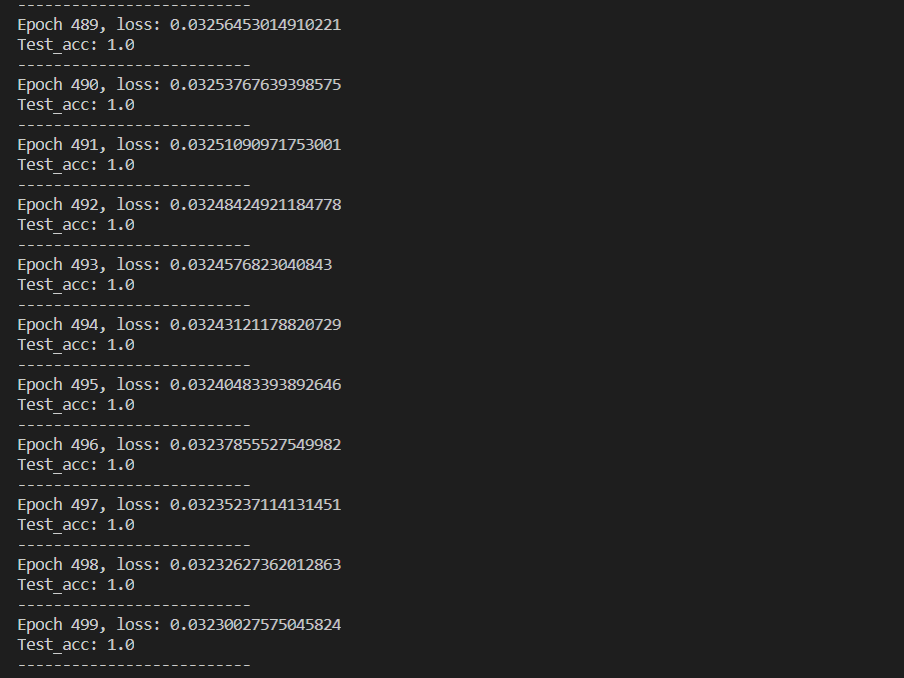
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 预测部分
print("*******predict*******")
# xx在-3到3之间以步长为0.01,yy在-3到3之间以步长0.01,生成间隔数值点
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
# 将xx, yy拉直,并合并配对为二维张量,生成二维坐标点
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
# 将网格坐标点喂入神经网络,进行预测,probs为输出
probs = []
for x_predict in grid:
# 使用训练好的参数进行预测
h1 = tf.matmul([x_predict], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2 # y为预测结果
probs.append(y)
# 取第0列给x1,取第1列给x2
x1 = x_data[:, 0]
x2 = x_data[:, 1]
# probs的shape调整成xx的样子
probs = np.array(probs).reshape(xx.shape)
plt.scatter(x1, x2, color=np.squeeze(Y_c))
# 把坐标xx yy和对应的值probs放入contour<[‘kɑntʊr]>函数,给probs值为0.5的所有点上色 plt点show后 显示的是红蓝点的分界线
plt.contour(xx, yy, probs, levels=[.5])
plt.show()
# 读入红蓝点,画出分割线,包含正则化
# 不清楚的数据,建议print出来查看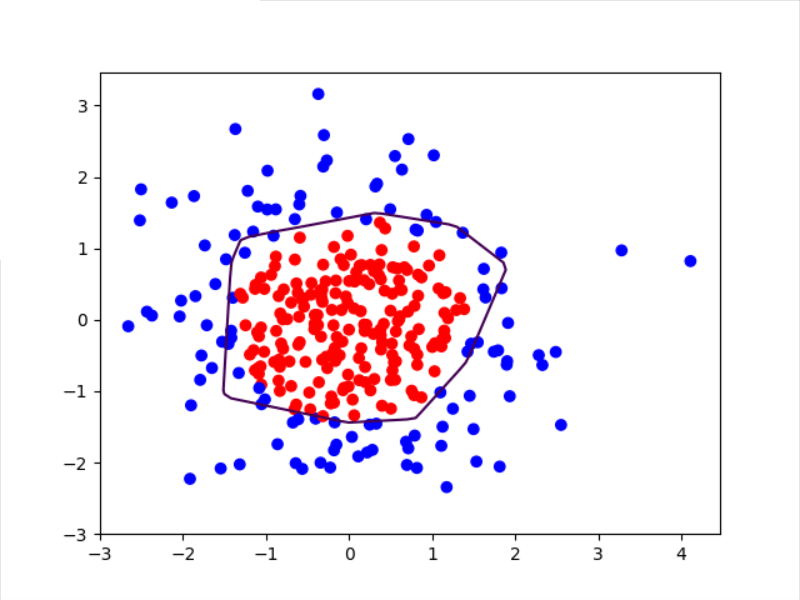
5 tensorflow实现寻找$loss=(w+1)^2$的最小值
1 | import tensorflow as tf |
6 张量





6.1 创建一个Tensor
1 | import tensorflow as tf |

1 | import tensorflow as tf |

1 | import tensorflow as tf |

1 | import tensorflow as tf |
6.2 numpy类型 < ---------- >tensor类型
1 | import tensorflow as tf |
7 tensorflow常用函数

1 | import tensorflow as tf |


1 | import tensorflow as tf |


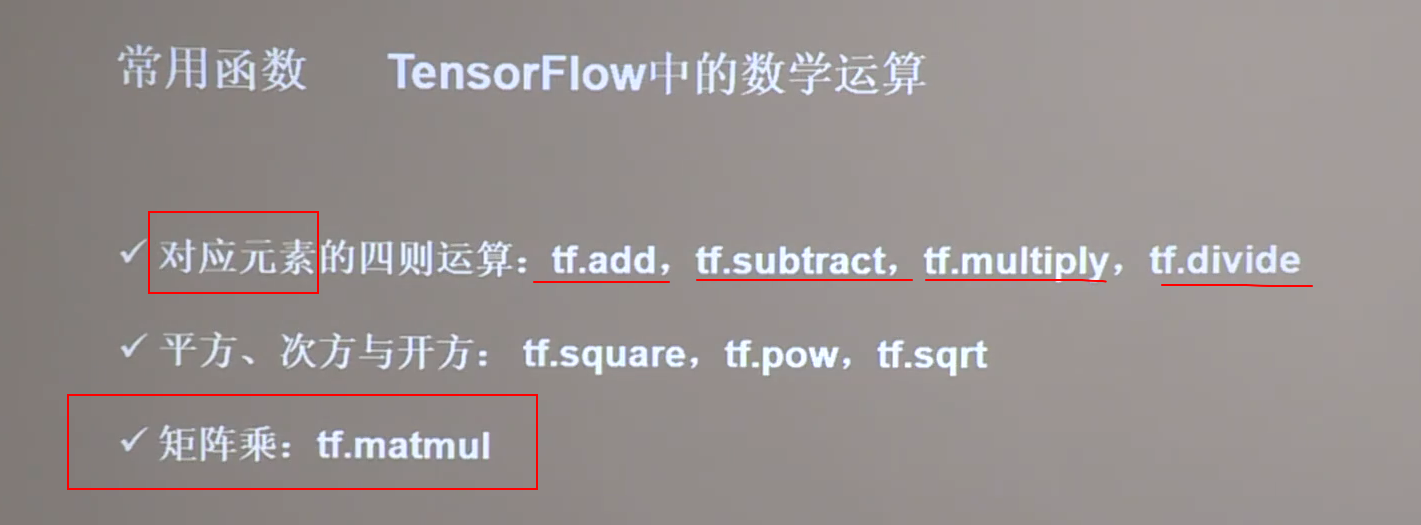
1 | import tensorflow as tf |


1 | import tensorflow as tf |


1 | import tensorflow as tf |


1 | import tensorflow as tf |


1 | import tensorflow as tf |


1 | seq = ['one', 'two', 'three'] |


1 | import tensorflow as tf |



-
假设输出y中的值都很大的时候,由于有指数运算可能导致计算机溢出,一个好的解决办法是找出输出y中的最大值,让y中的每一个元素都减去这个最大值,再把处理后的y送给softmax函数。
1 | import tensorflow as tf |


1 | import tensorflow as tf |


1 | import numpy as np |


1 | import tensorflow as tf |


1 | import numpy as np |


1 | import numpy as np |

1 | import numpy as np |
8 鸢尾花数据集的读入


1 | from sklearn import datasets |
9 神经网络实现鸢尾花分类

1 | # -*- coding: UTF-8 -*- |

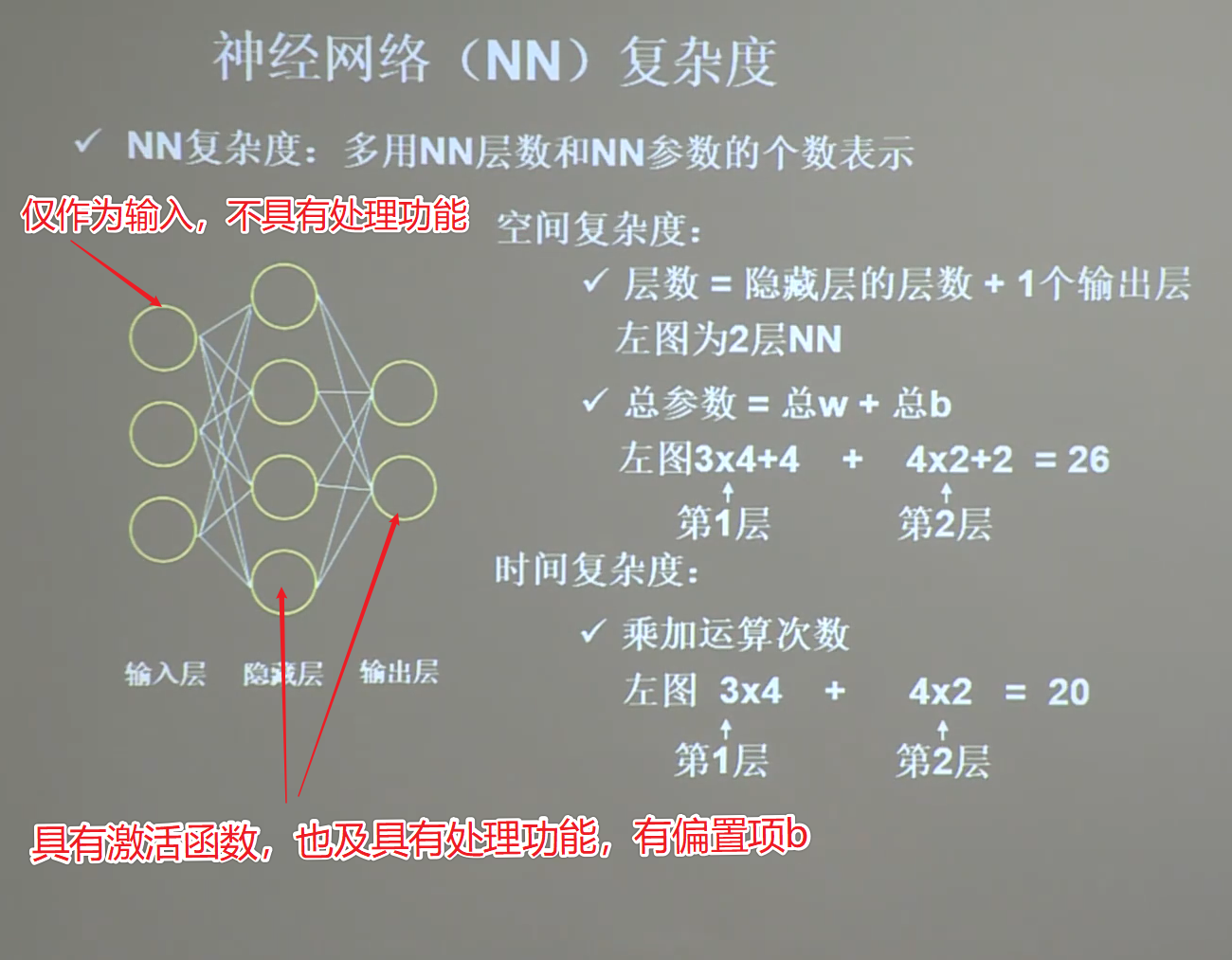
10 神经网络复杂度
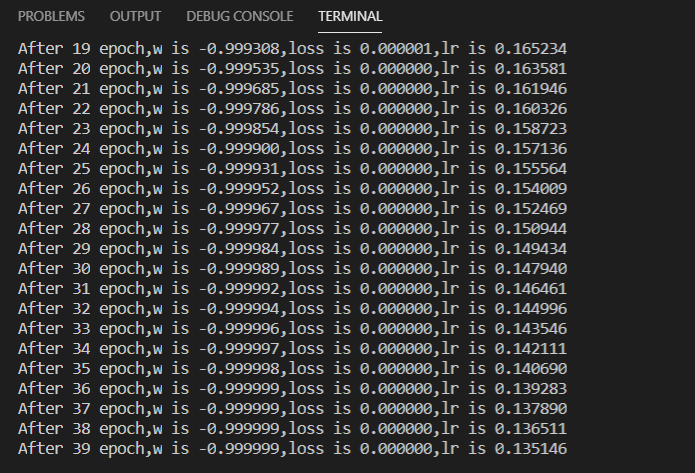
11 指数衰减学习率

1 | import tensorflow as tf |
12 损失函数

预测酸奶销量$y$, $x_1$和$x_2$是影响酸奶销量的因素。
建模前,应预先采集的数据集有:每日$x_1$、$x_2$和销量$y$。(即已知答案,最佳情况是产量等于销量)
拟造数据集$X,Y_$:
$y_=x_1+x_2$
噪声: $-0.05\thicksim+0.05$
要求:
拟合可以预测销量的函数.
-
使用$MSE$损失函数
1 | import tensorflow as tf |
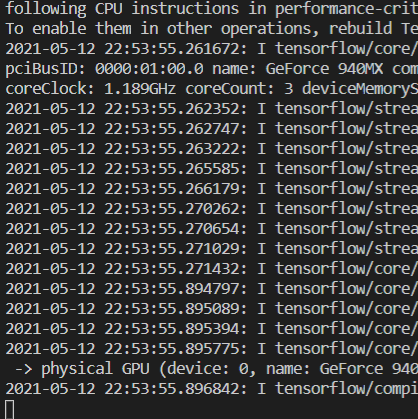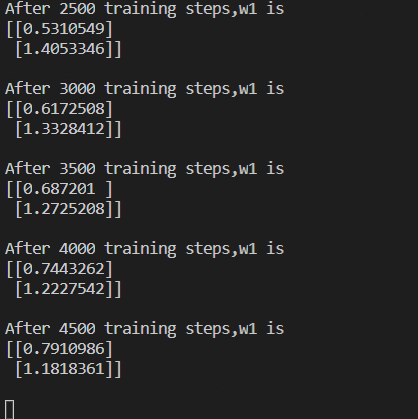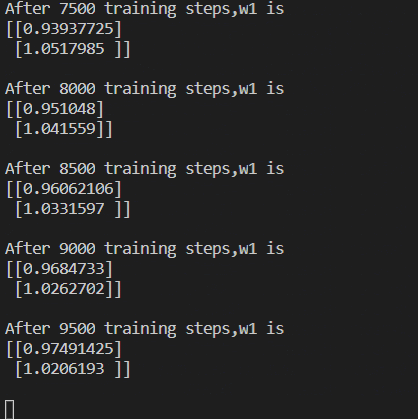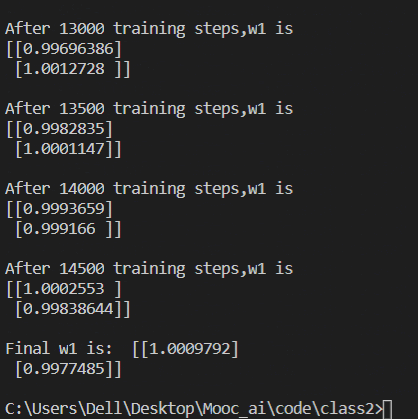
-
自定义损失函数

1 | import tensorflow as tf |
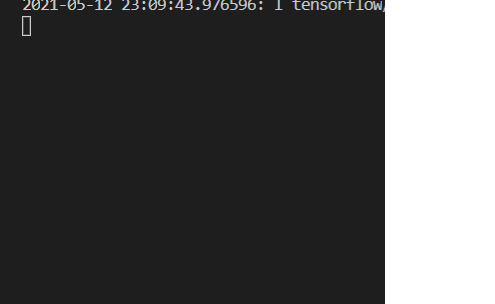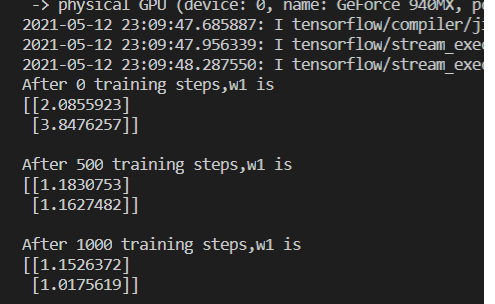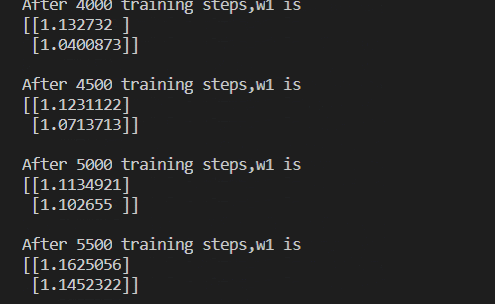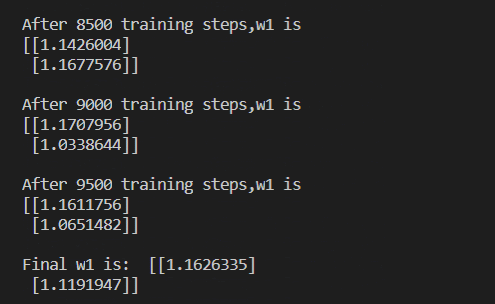
13 交叉熵损失函数
-
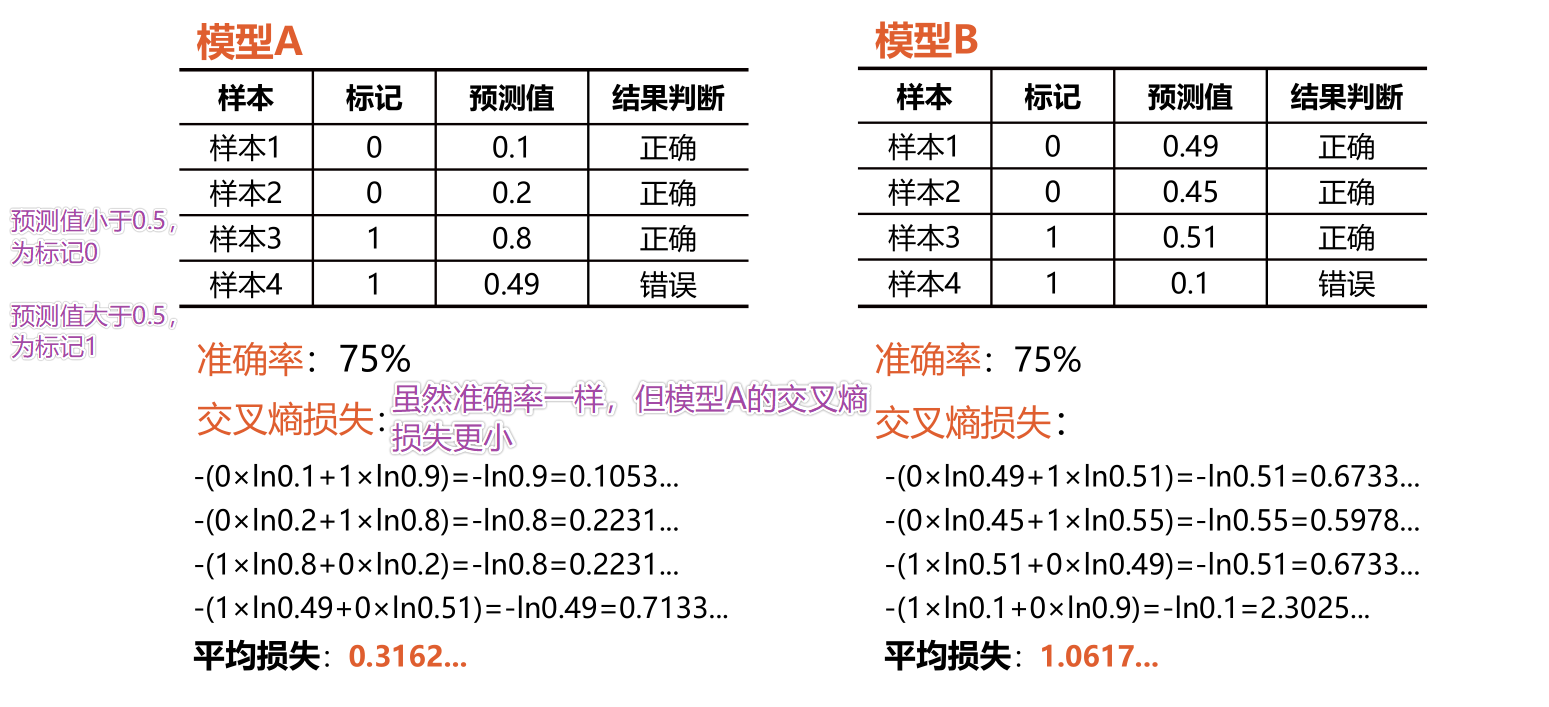
交叉熵是一个信息论中的概念,它原来是用来估算平均编码长度的。如果用在概率分布中,比如给定两个概率分布p和q,通过q来表示p的交叉熵如下图所示:
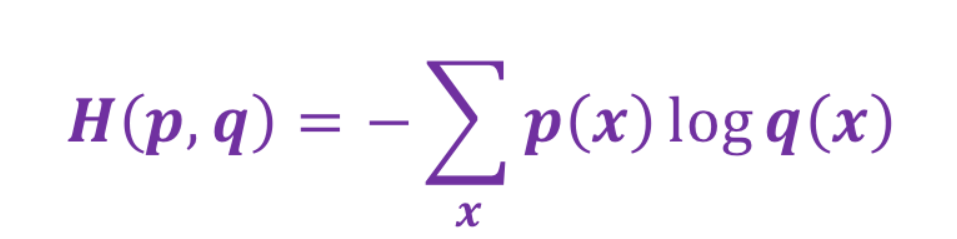
交叉熵刻画的是两个概率分布之间的距离,p代表正确答案,q代表的是预测值,交叉熵越小,两个概率的分布约接近,损失越低。对于机器学习中的多分类问题,通常用交叉熵做为损失函数。
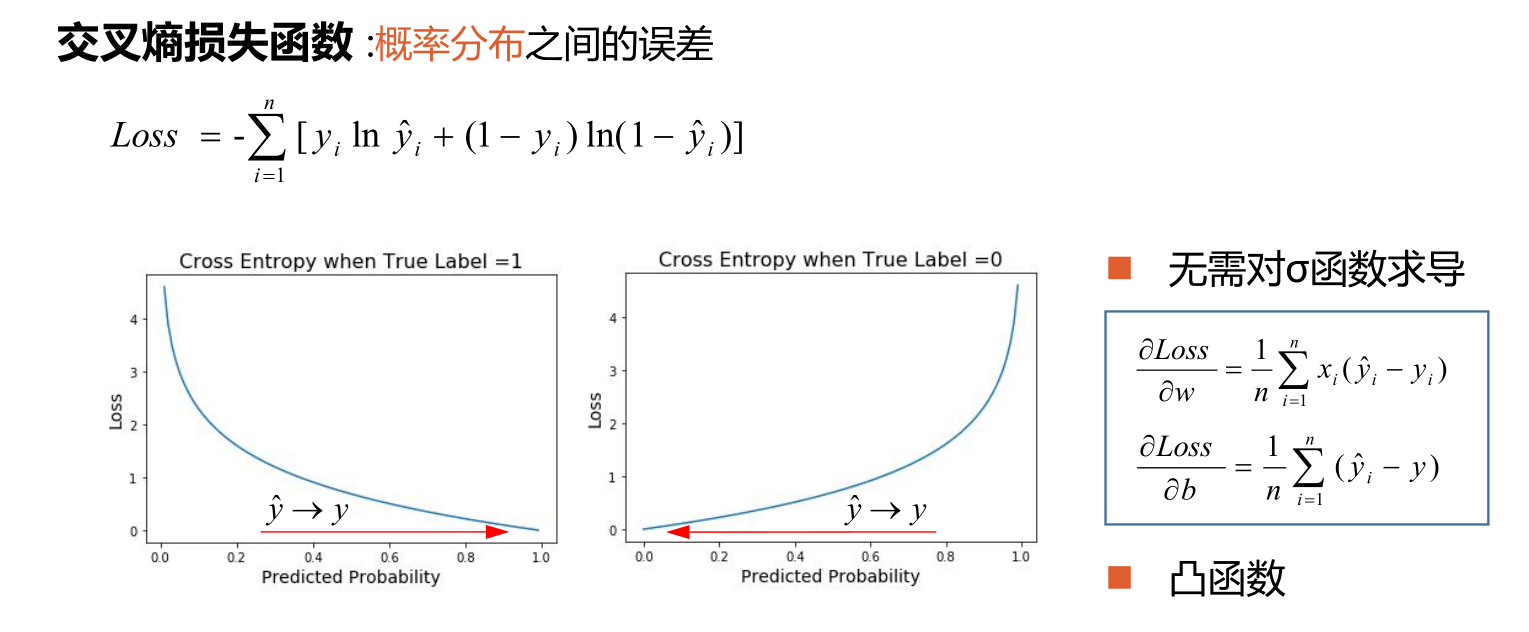
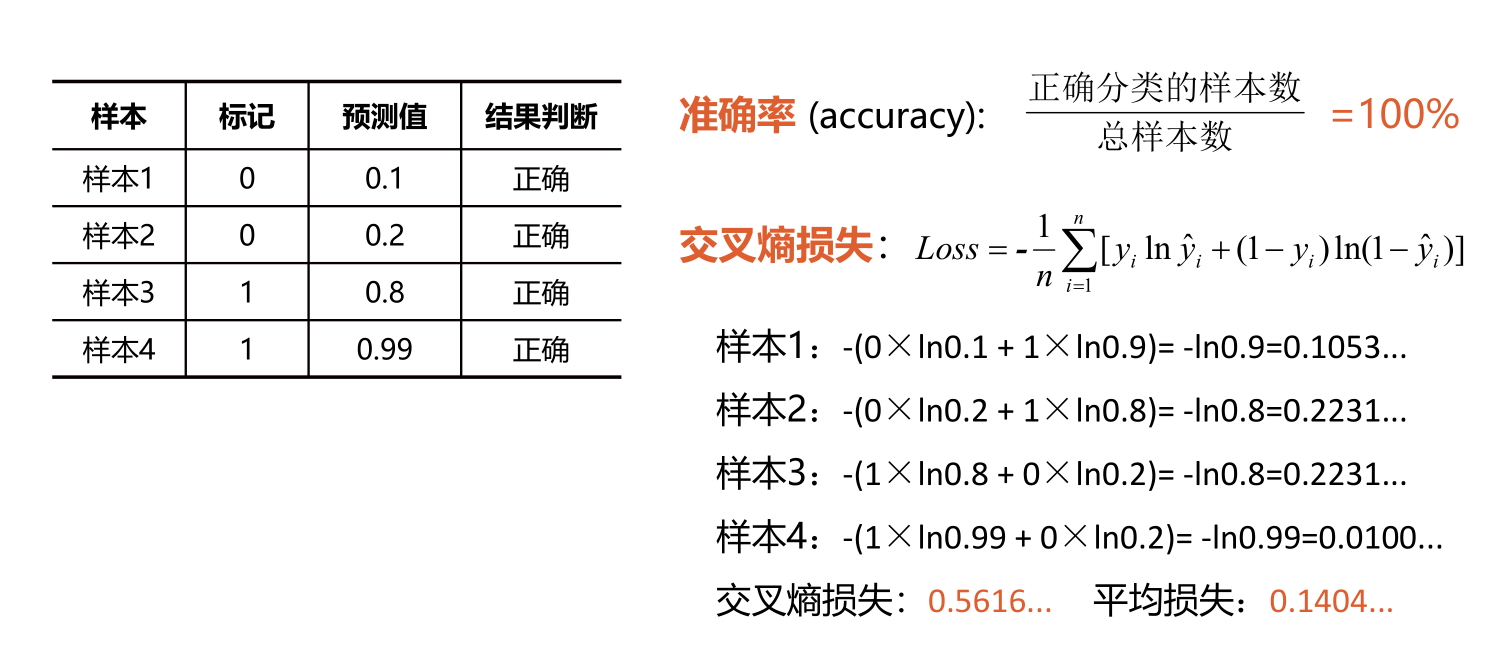

1 | import tensorflow as tf |


1 | # softmax与交叉熵损失函数的结合 |
14 神经网络优化器——引导神经网络更新参数

不同的优化器只是$m_t$和$V_t$不同
14.1 SGD (Stochastic Gradient Descent)

1 | w1.assign_sub(lr * grads[0]) # 参数w1自更新 |
14.2 SGDM

1 | m_w, m_b = 0, 0 |
14.3 Adagrad

1 | v_w, v_b = 0, 0 |
14.4 RMSProp

1 | v_w, v_b = 0, 0 |
14.5 Adam

1 | m_w, m_b = 0, 0 |
15 tf.keras搭建网络
用TensorFlow API:tf.keras搭建网络八步法:
-
import
-
train,test
-
model = tf.keras.models.Sequential 描述网络结构
-
model.compile 配置训练方法,优化器,损失函数,评测指标
-
model.fit 执行训练过程 batch 要迭代多少次
-
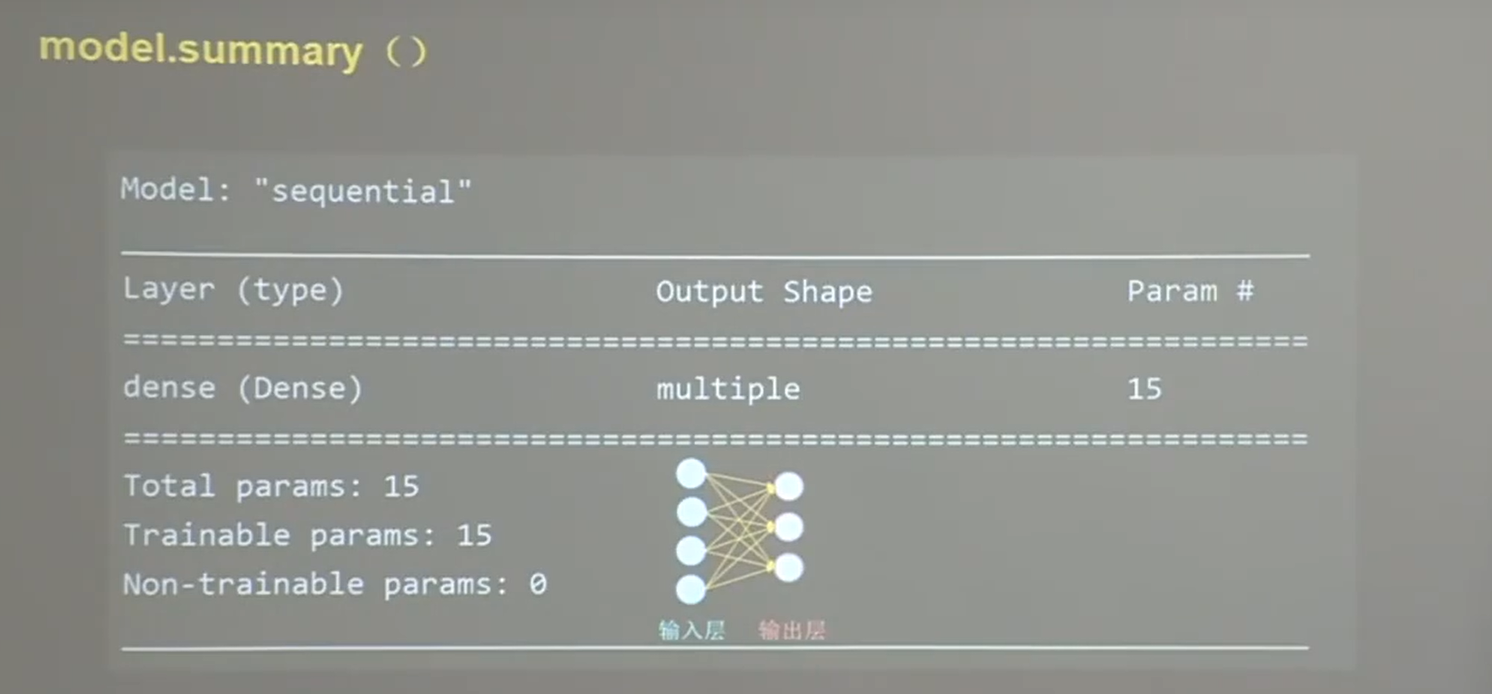
model.summary 打印网络结构和参数统计
1 | # tf.keras.models.Sequential([网络结构]) |
1 | # model.compile(optimizer=优化器, |
1 | # model.fit(训练集的输入特征, 训练集的标签 |
16 tf.keras实现鸢尾花分类
1 | import tensorflow as tf |
17 使用tf.keras 类实现鸢尾花分类
1 | import tensorflow as tf |
18 MNIST数据集

1 | import tensorflow as tf |
18.1 tf.keras 实现手写数字识别
1 | import tensorflow as tf |
18.2 tf.keras 类 实现手写数字识别
1 | import tensorflow as tf |
19 FASHION数据集

19.2 tf.keras 实现FASHION数据集的神经网络训练
1 | import tensorflow as tf |
19.2 tf.keras 类 实现FASHION数据集的神经网络训练
1 | import tensorflow as tf |
20 tf.keras搭建神经网络的延申
20.1 自制数据集,解决本领域应用
-
之前都是用的别人写好的
1 | mnist = tf.keras.datasets.mnist |
-
自己写个函数把load_data()替换掉
1 | # 训练集图片路径 |
20.2 数据增强,扩展数据集,提高泛化力
数据增强:Data Augumentation
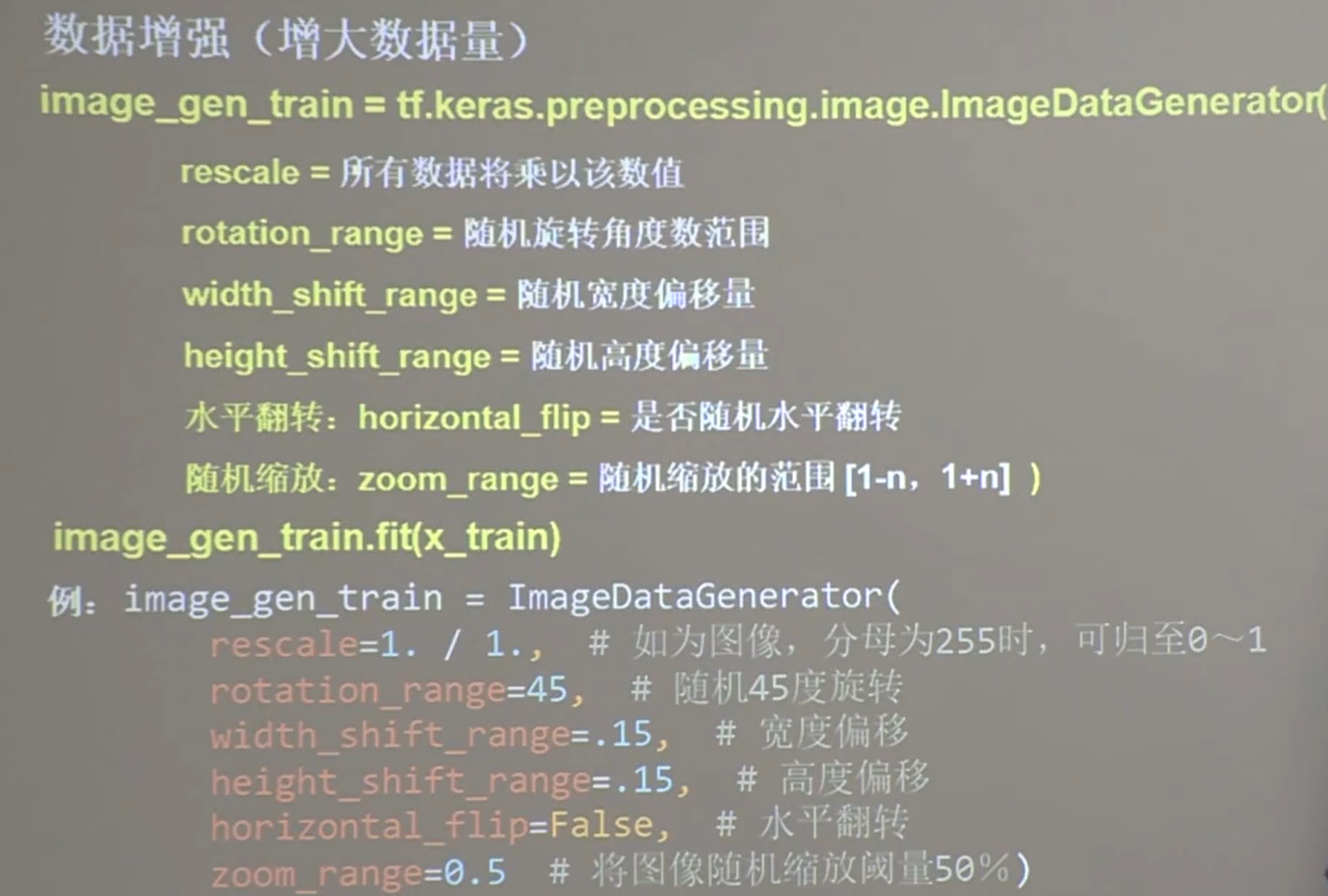

1 | model.fit(image_gen_train.flow(x_train, y_train, batch_size=32), epochs=5, validation_data=(x_test, y_test), |
20.3 断点续训,实时保存最优模型,存取模型
使用回调函数callbacks=[cp_callback] 实现断点续训
1 | checkpoint_save_path = "./checkpoint/mnist.ckpt" |
20.4 参数提取,把参数存入文本

1 | # model.trainable_variables 返回模型中可训练的参数 |
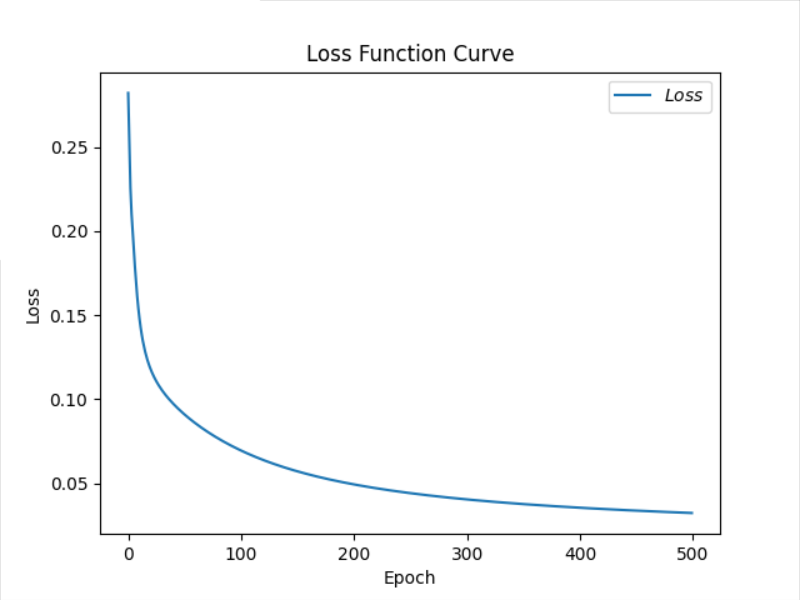
20.5 acc/loss可视化,见证模型的优化过程
1 |
|
20.6 应用程序,给图识物
在这个阶段,往往要对现实中输入的图片进行“预处理”,譬如MINIST数据集中是黑底白字,则需要将现实中的输入处理成黑底白字再送入神经网络。不进行预处理则效果很差。
1 | from PIL import Image |
21 卷积神经网络 CNN
卷积神经网络就是特征提取器: C B A P D



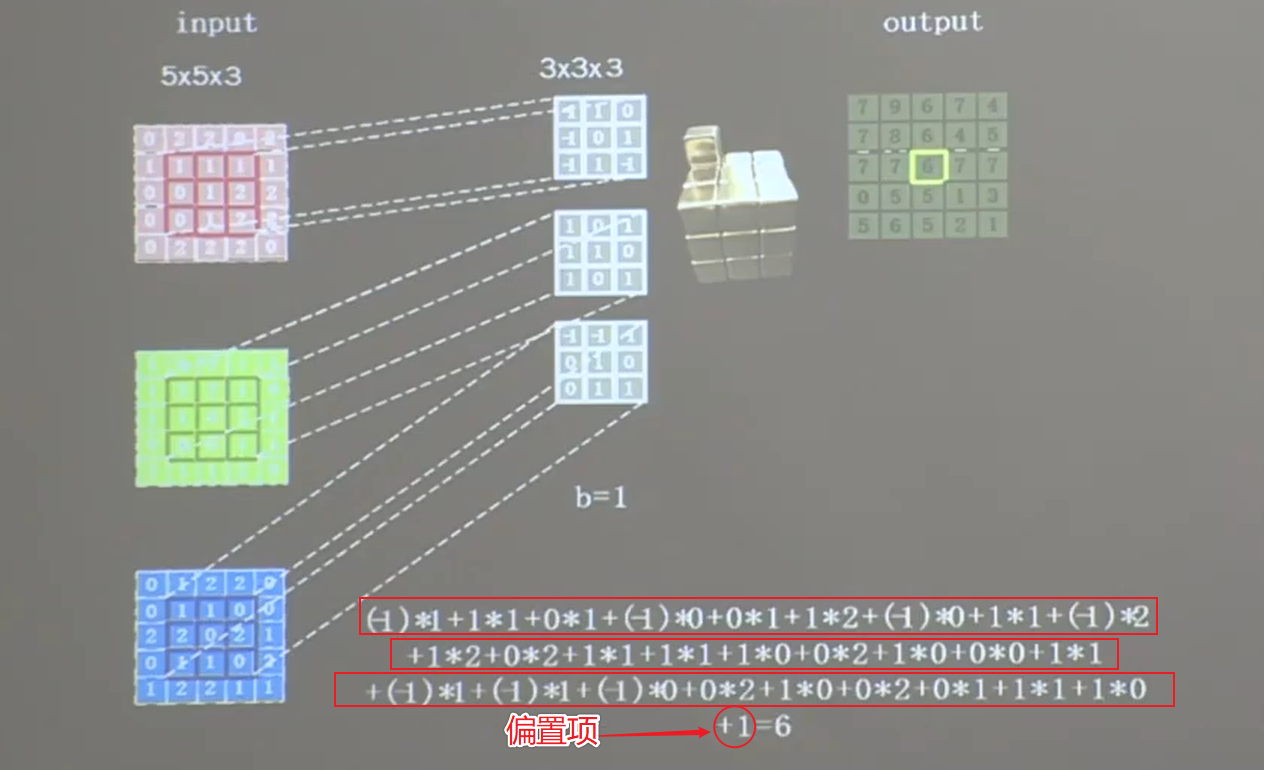
21.1 感受野
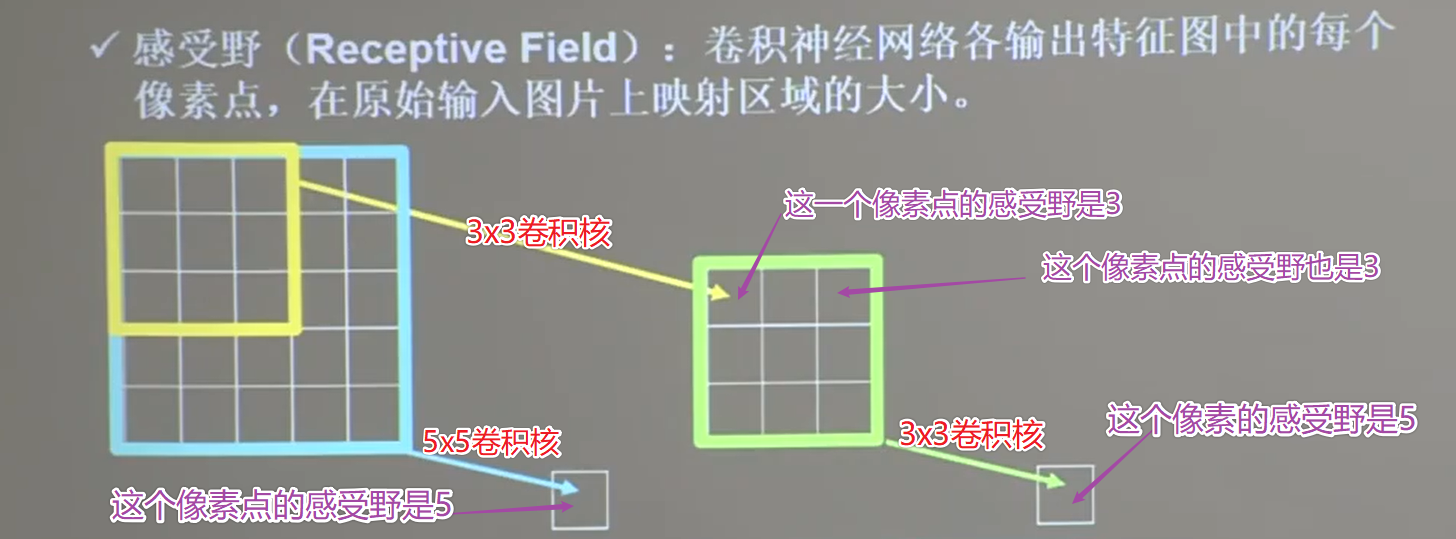
故两个3x3的卷积核的特征提取能力和一个5x5的卷积核的特征提取能力一样,哪个好?
经过卷积作用,输出多少个像素点? 每个像素点需要多少次乘加运算?
21.2 填充

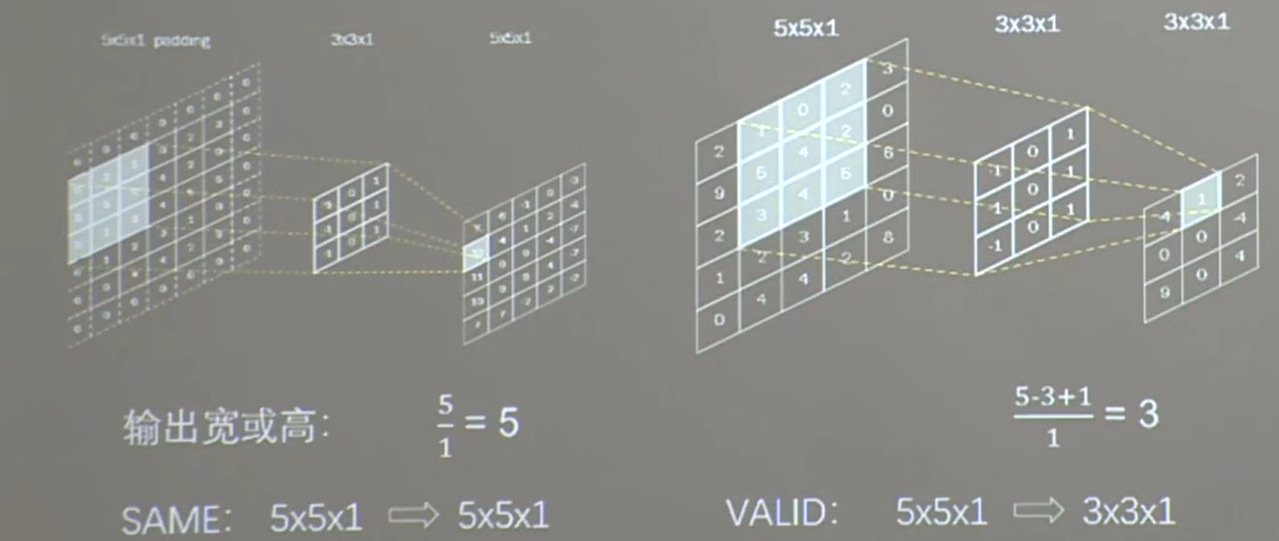
21.3 TF描述卷积层

21.4 Batch Normalization

为什么需要BN?
经过多层网络,数据有偏移
将数据重新拉回到N(0, 1),使进入激活函数的数据分布在激活函数的线性区,使得数据的微小变化更能体现到激活函数的输出,提升激活函数对输入数据的区分力
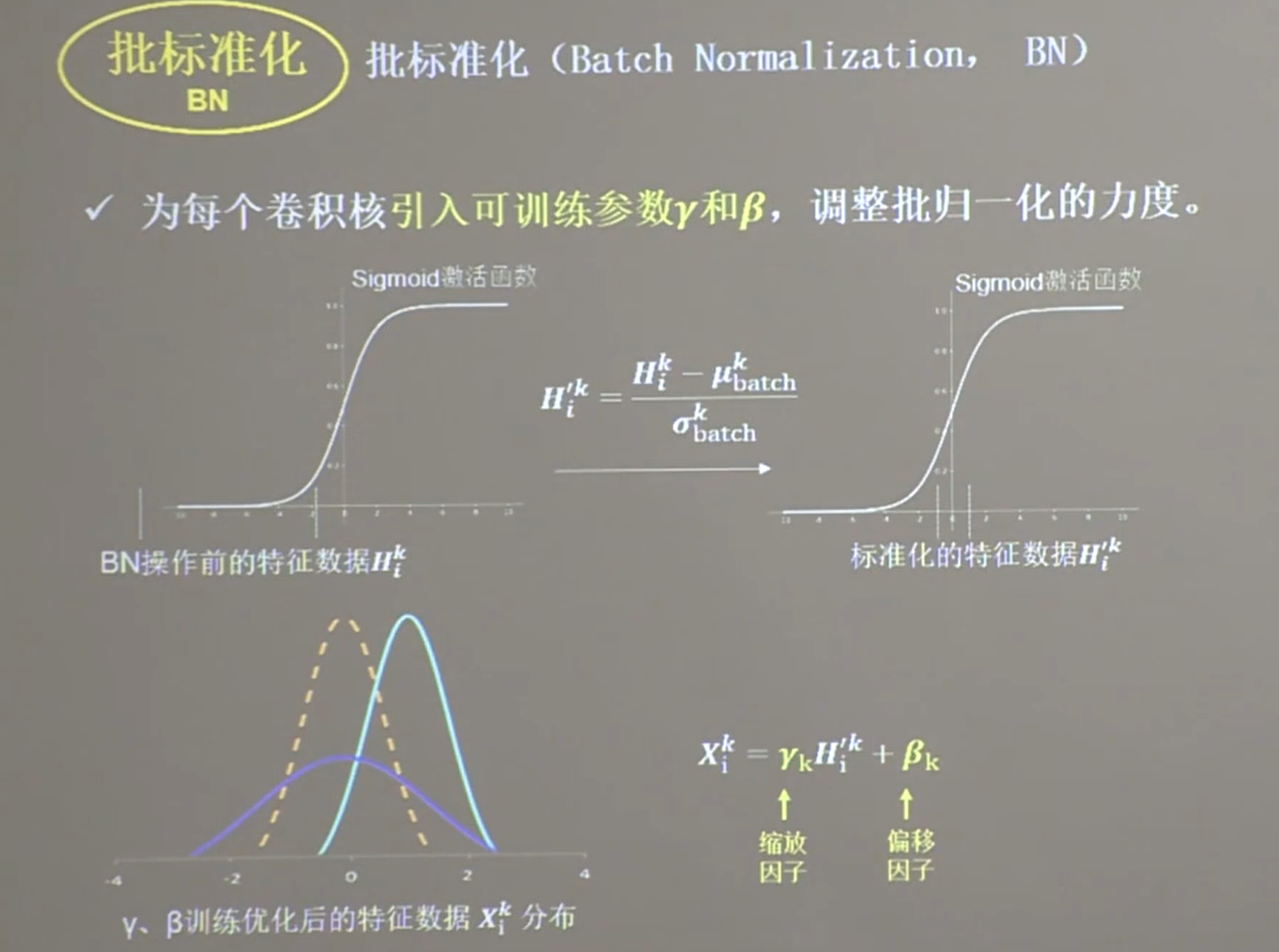
缩放因子和偏移因子是可训练参数,保证网络的非线性表达力

21.5 池化



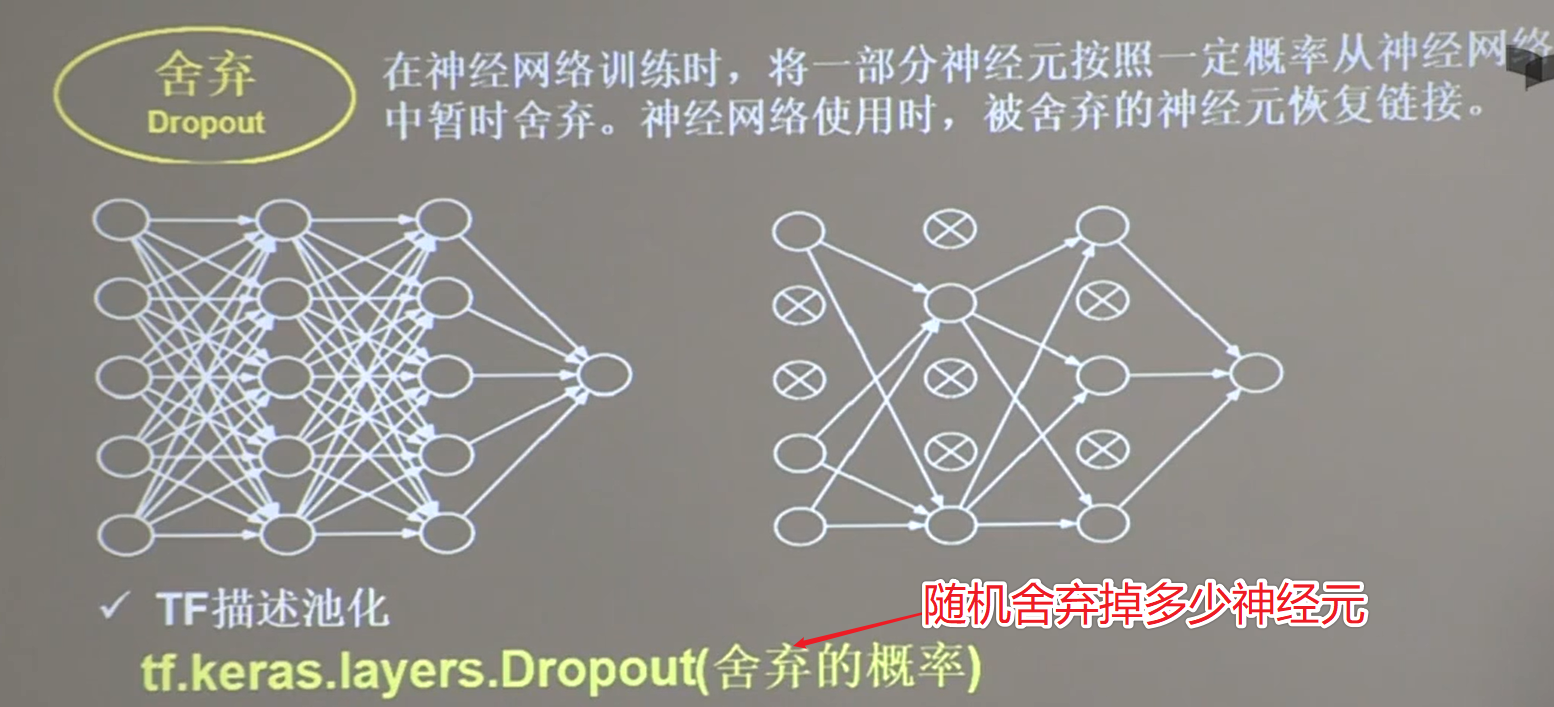
21.6 Dropout
22 Cifar10 数据集

23 卷积神经网络搭建示例
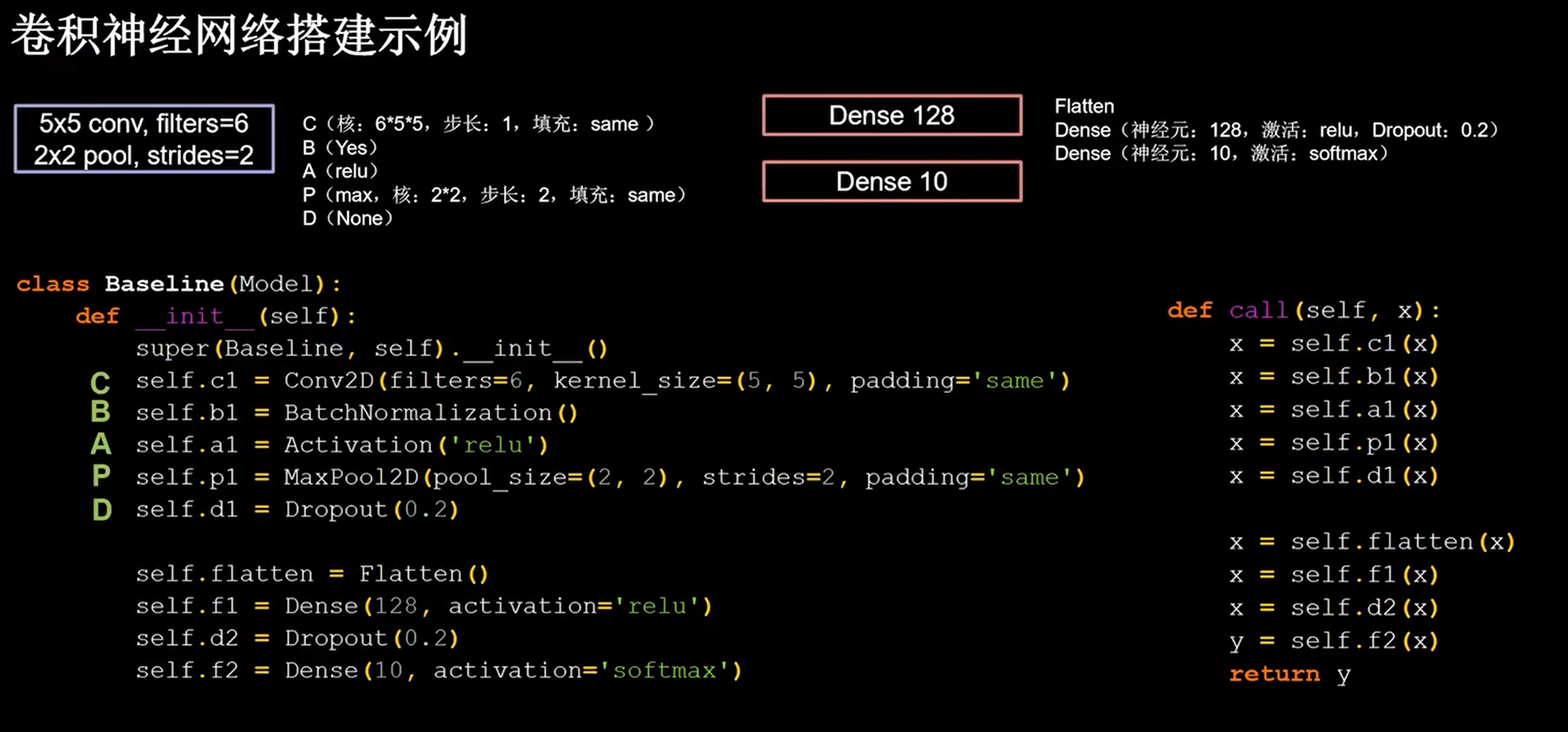
1 | import tensorflow as tf |
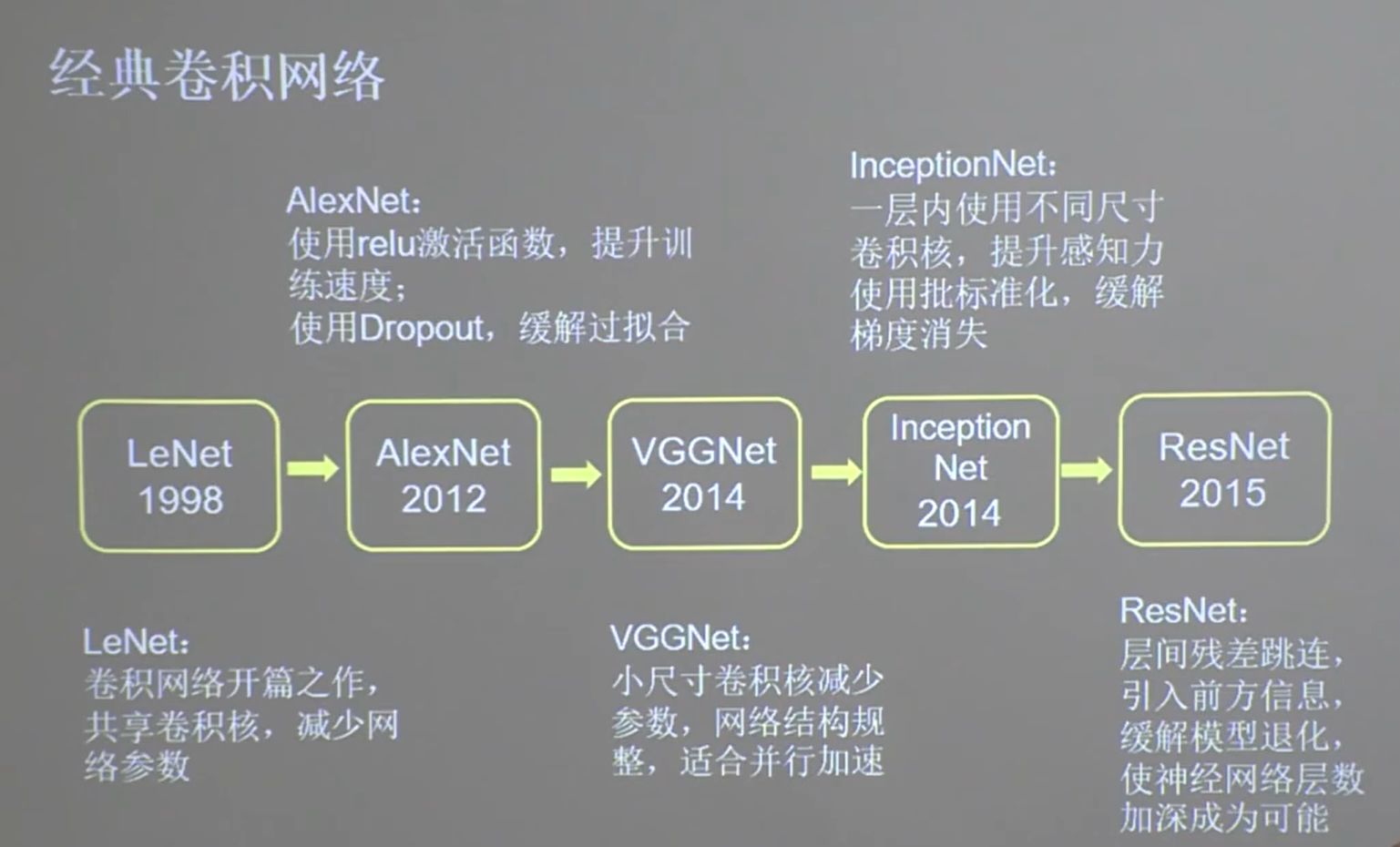
24 经典卷积神经网络

24.1 LeNet
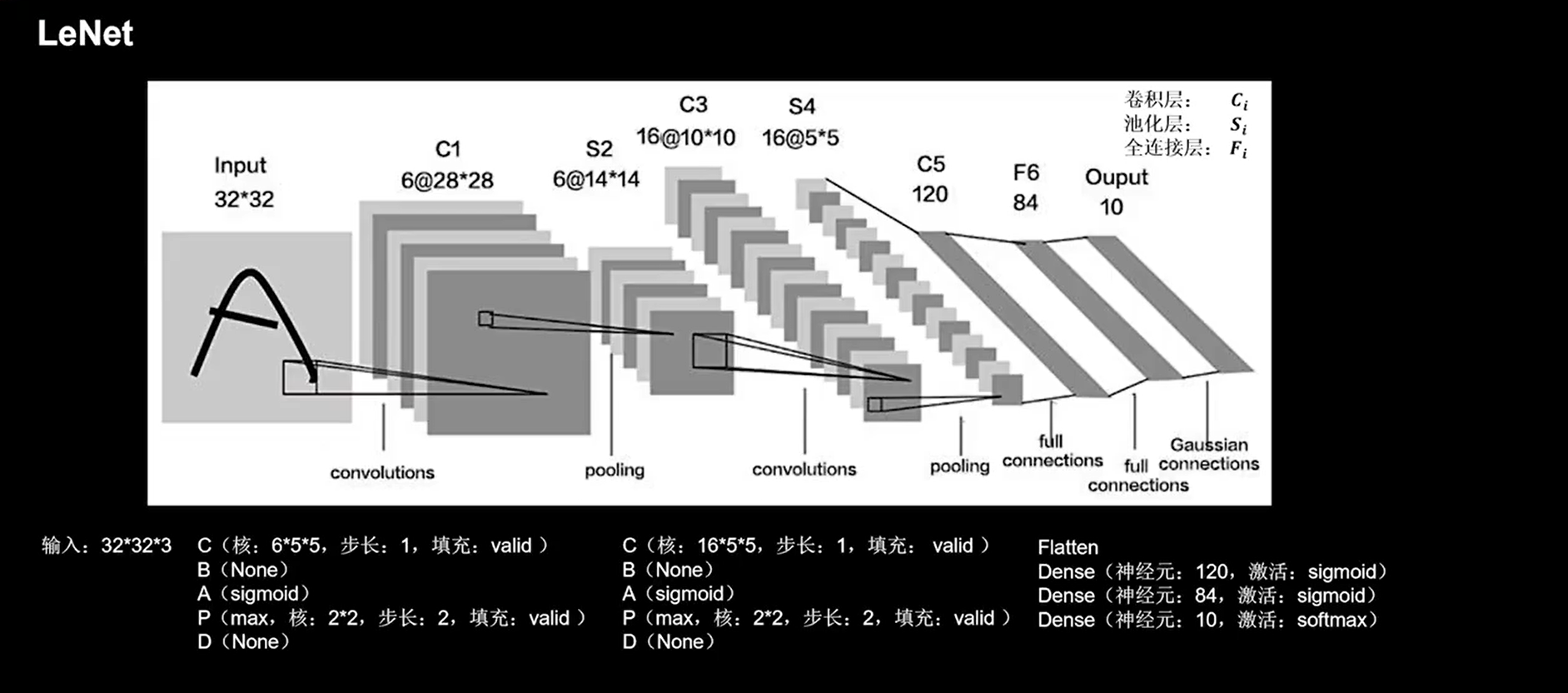
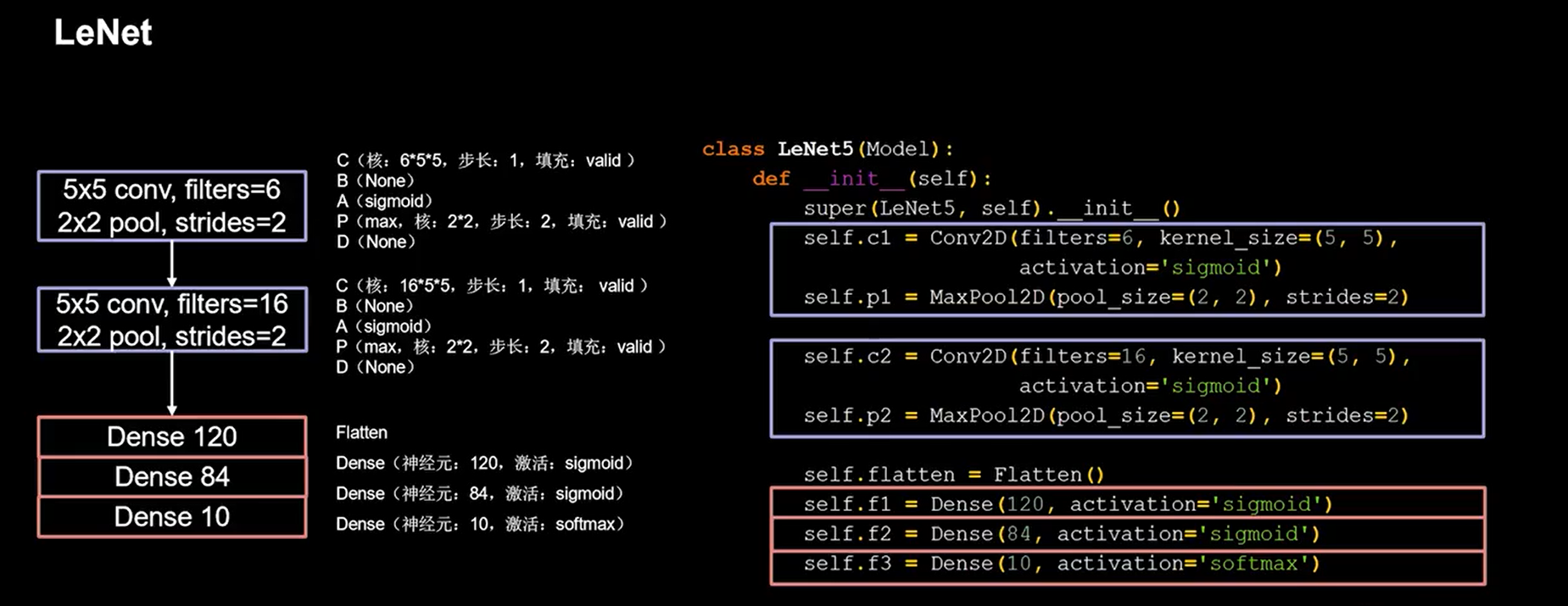
1 | class LeNet5(Model): |
24.2 AlexNet
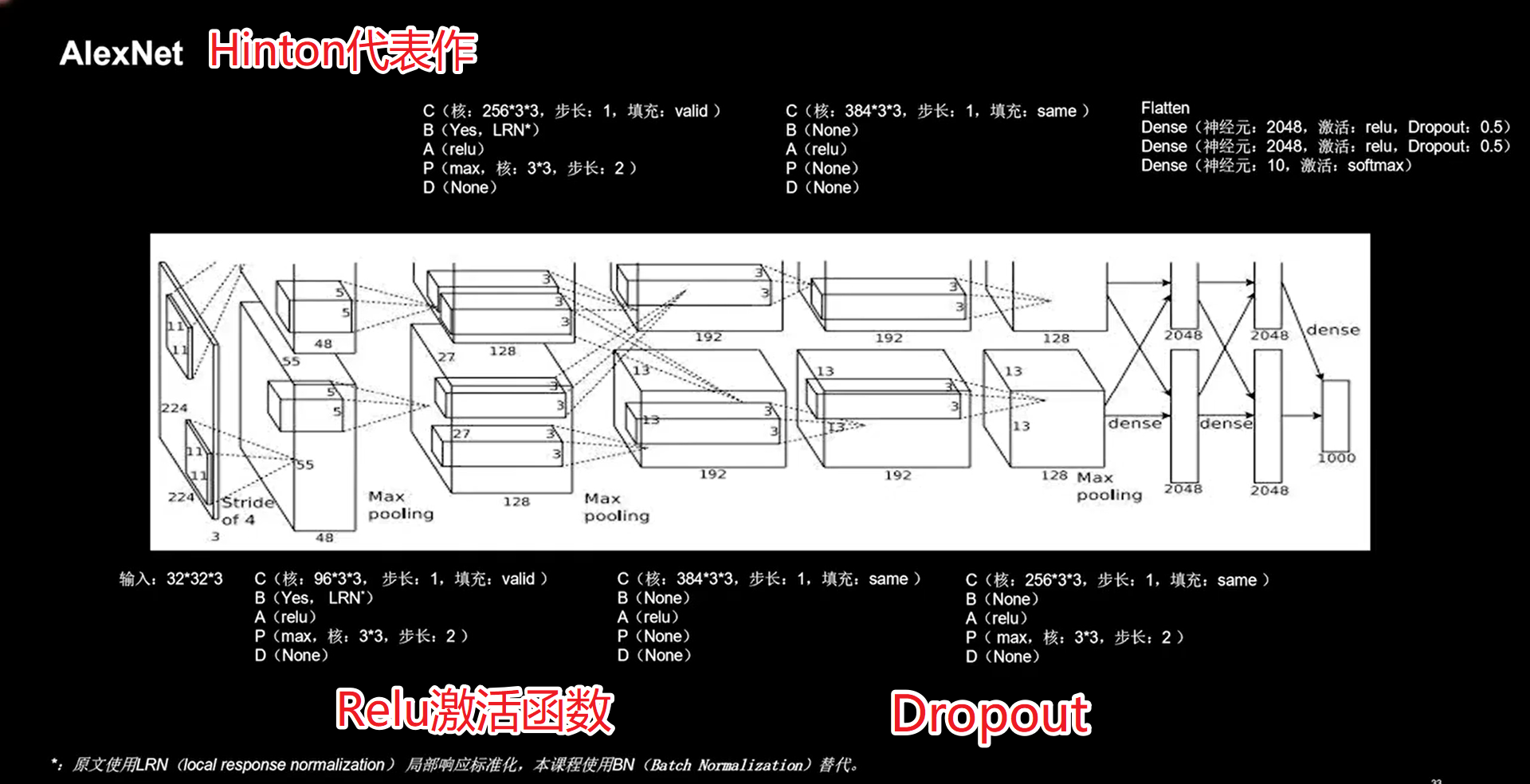
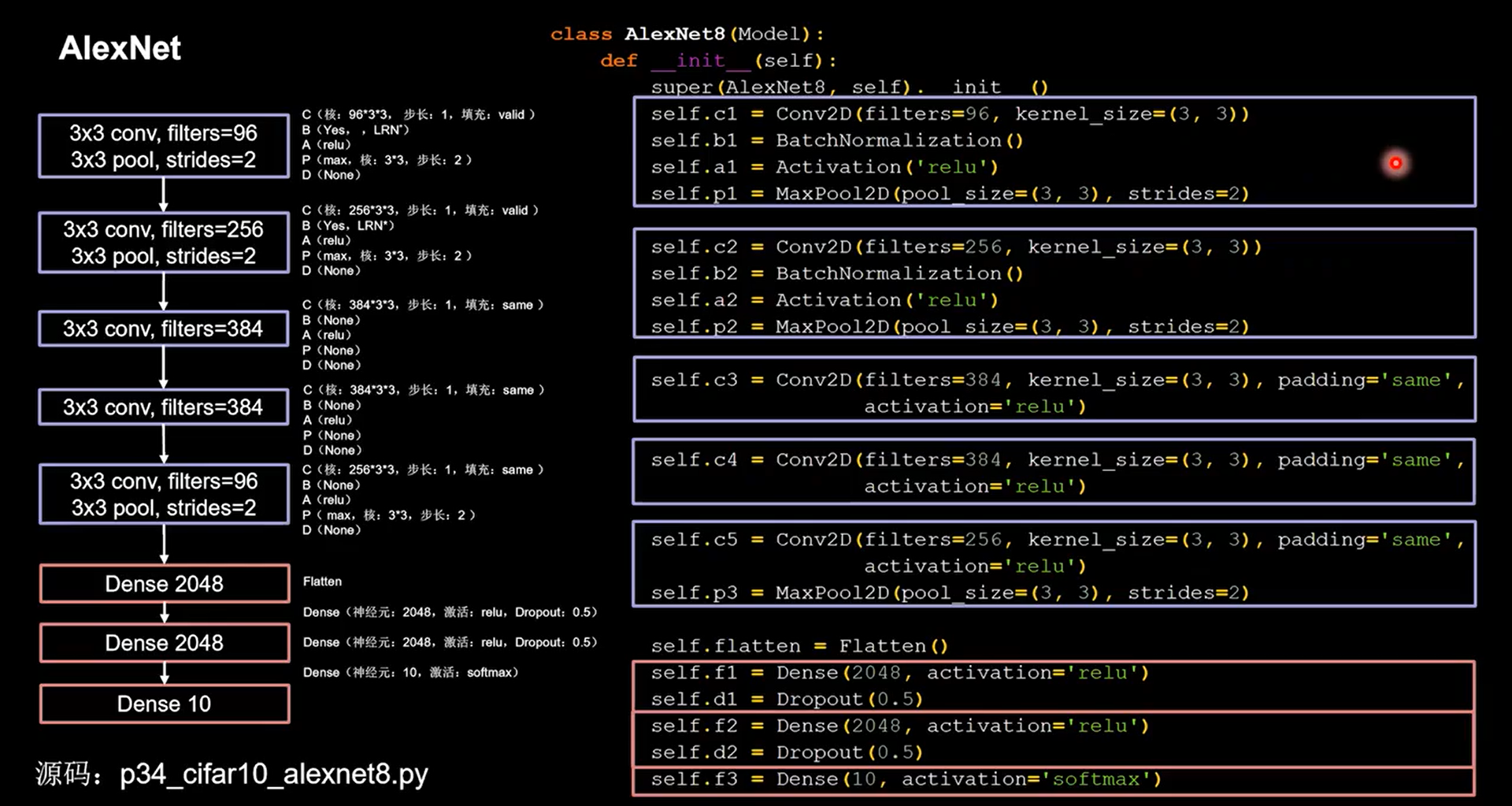
1 | class AlexNet8(Model): |
24.3 VGGNet
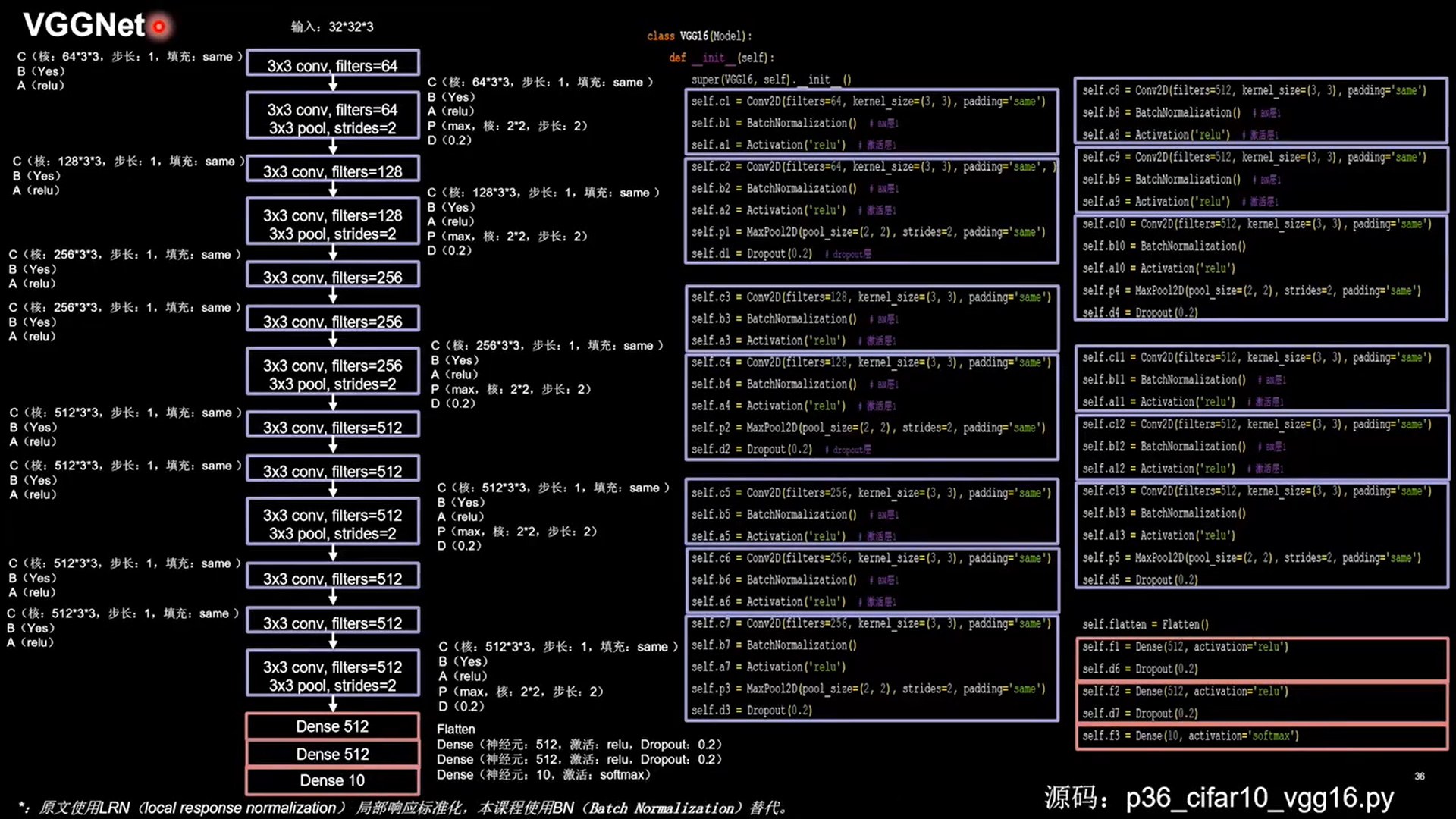
1 | class VGG16(Model): |
24.4 InceptionNet
-
引入了Inception结构块
-
在同一层网络内使用不同尺度的卷积核,提升了模型的感知力
-
使用了批标准化,缓解了梯度消失
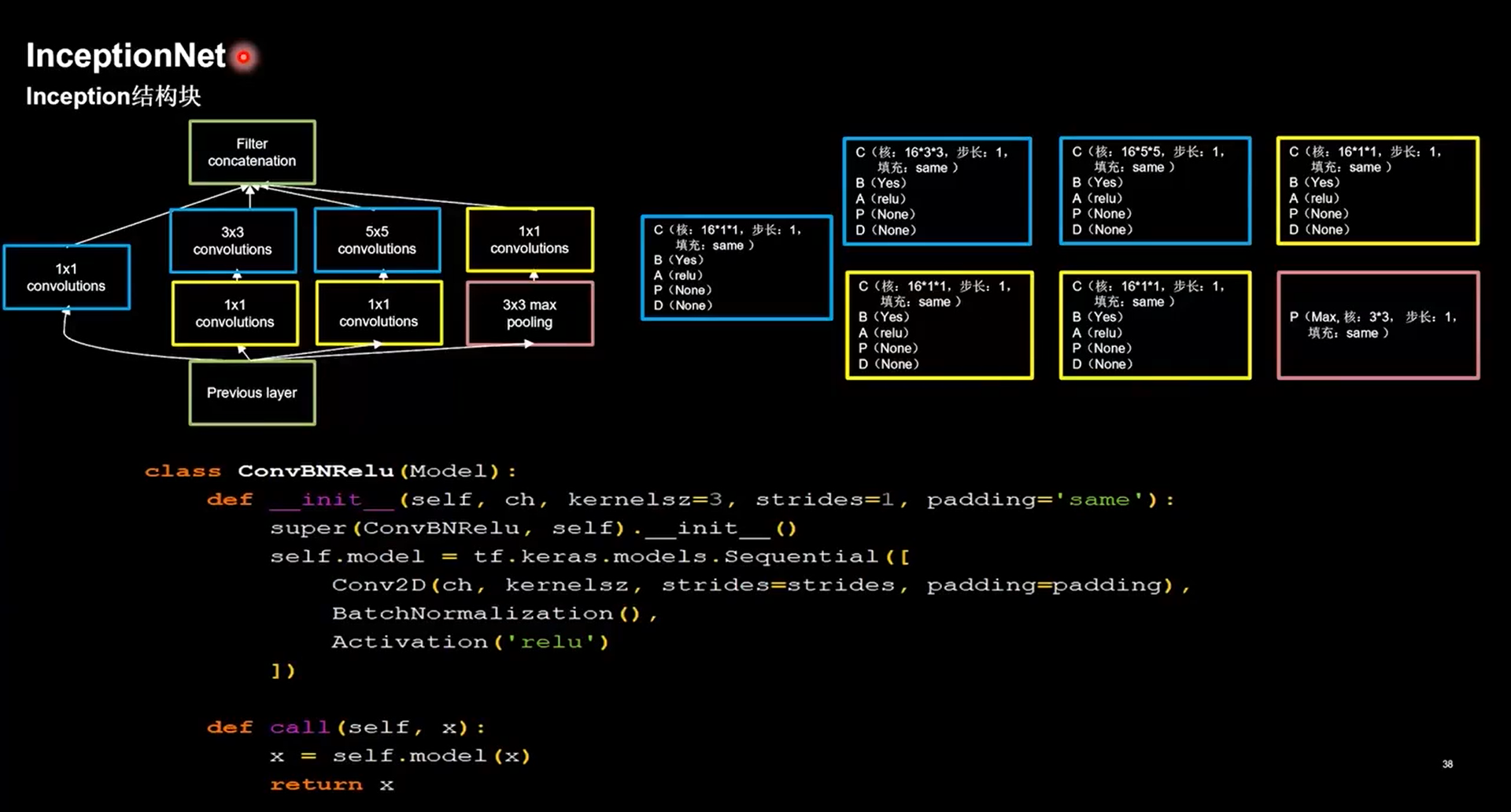
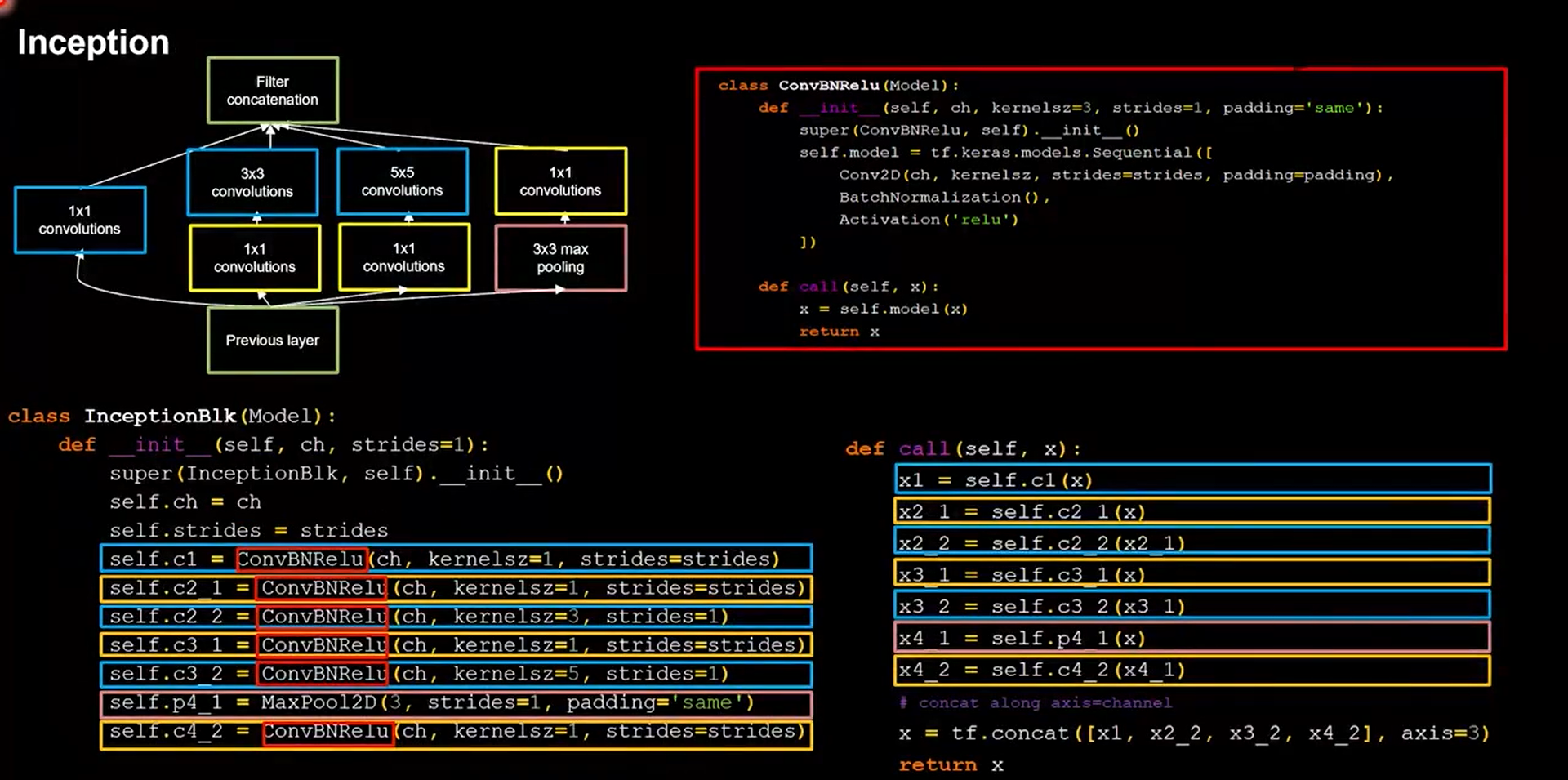
1 | class ConvBNRelu(Model): |
24.5 ResNet
-
层间残差跳连,引入前方信息,缓解梯度消失
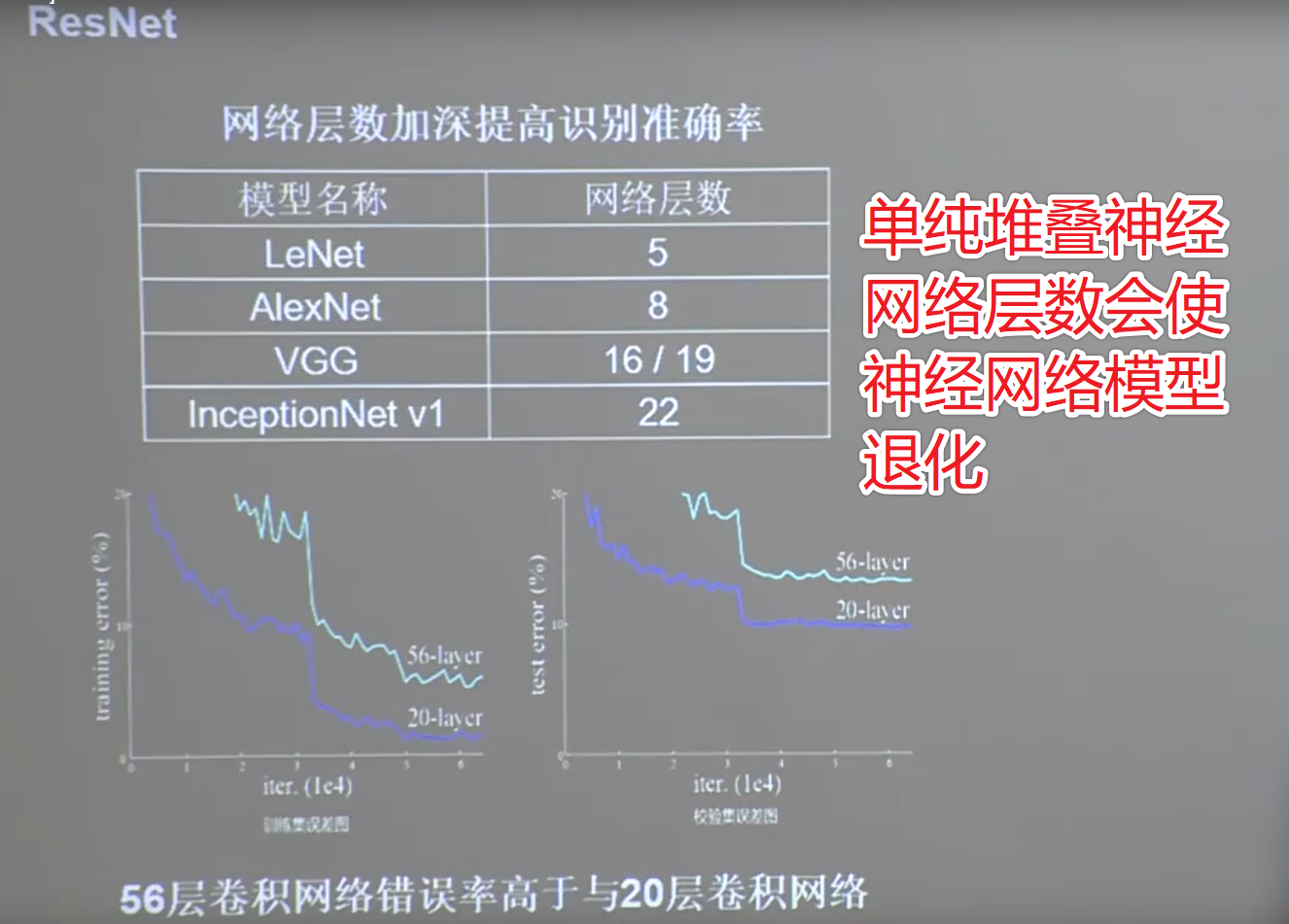
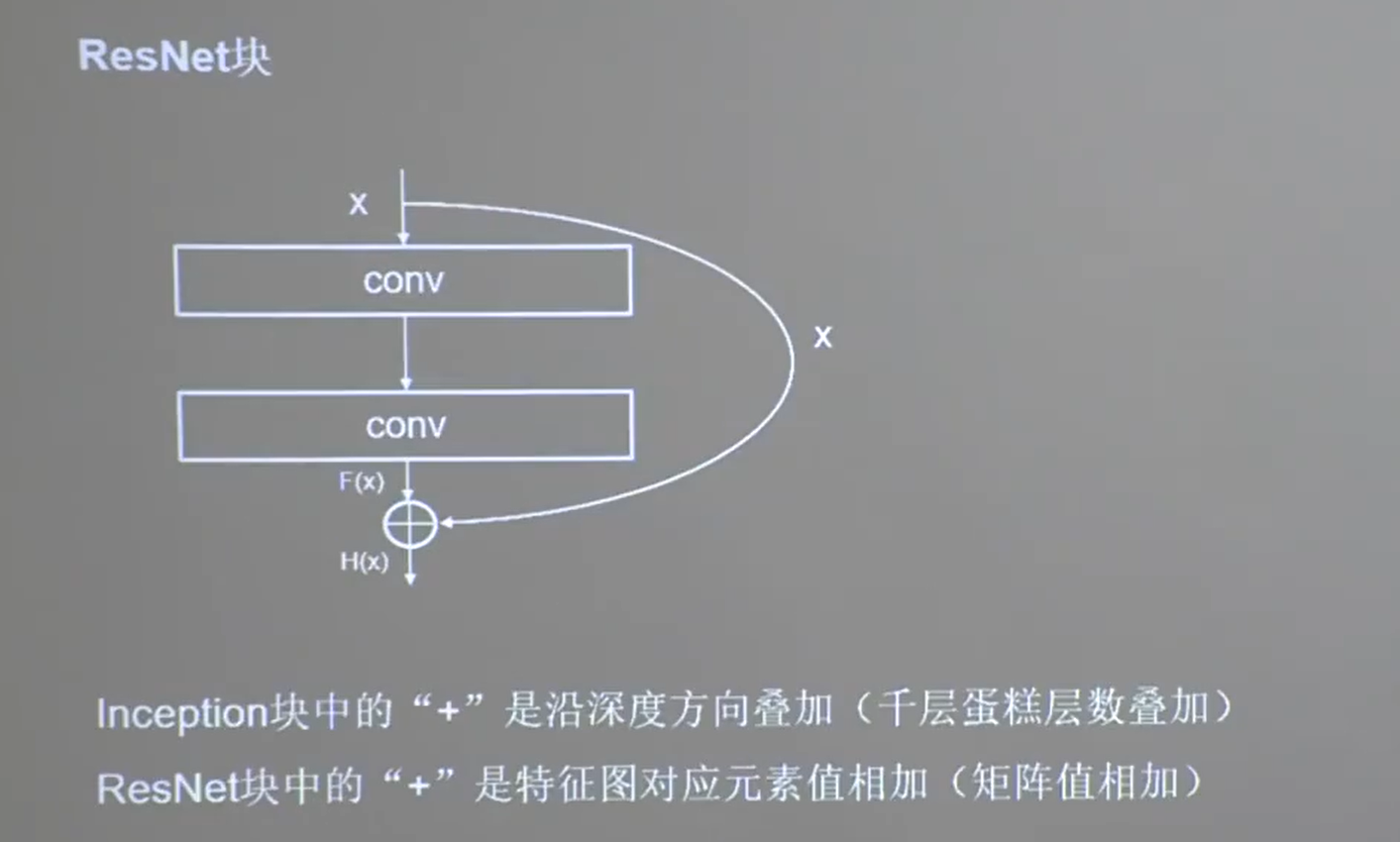
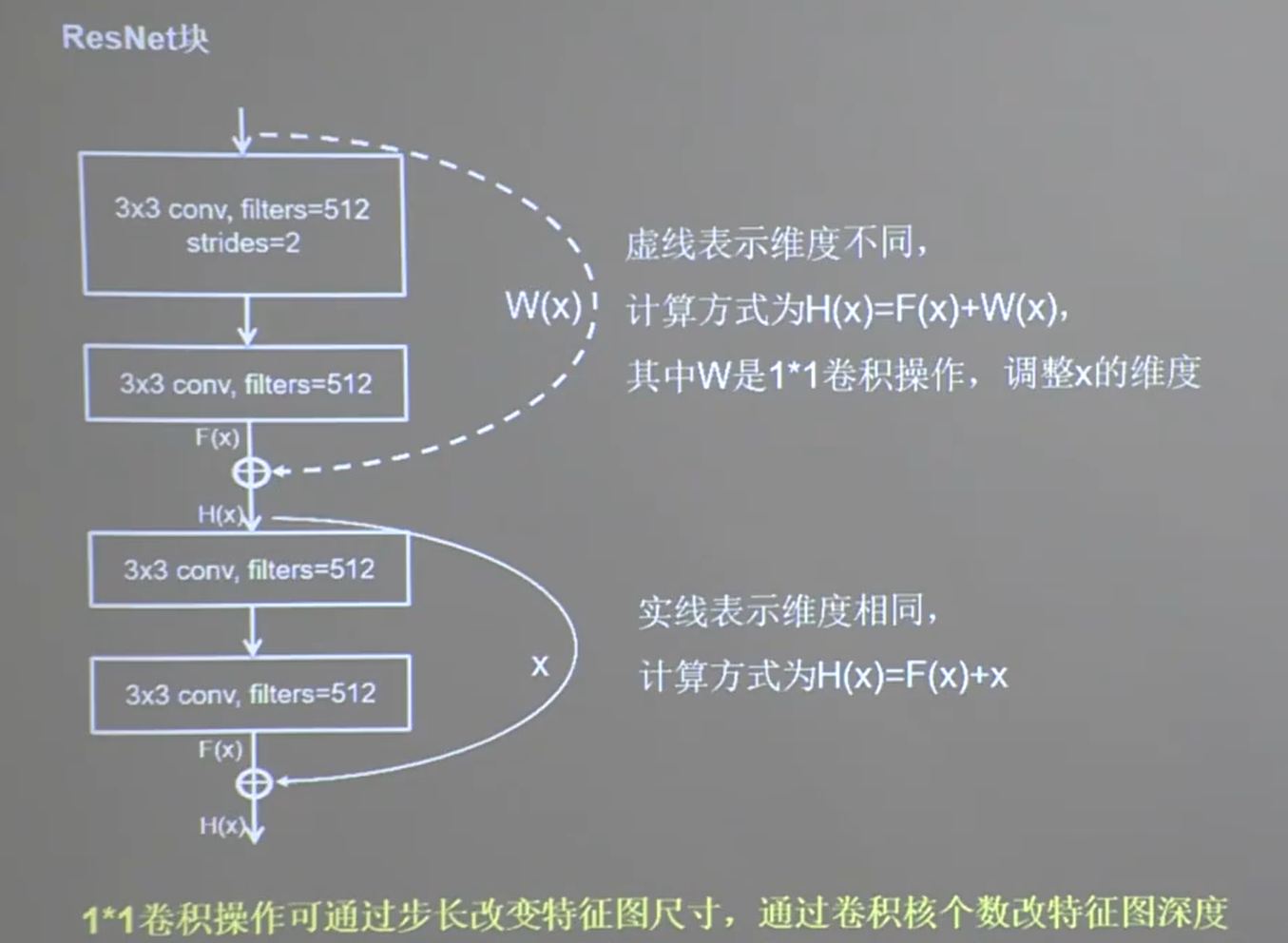
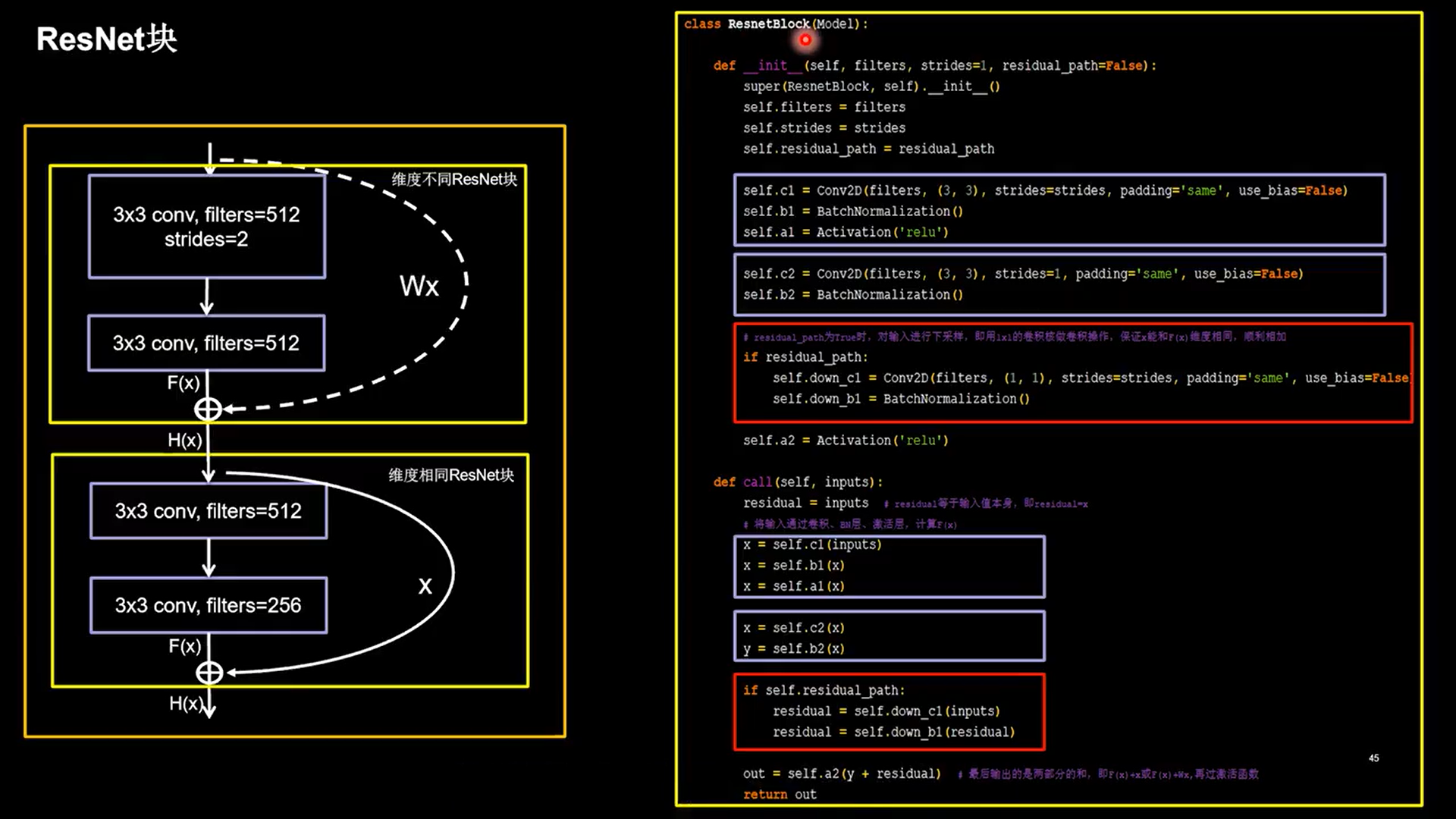
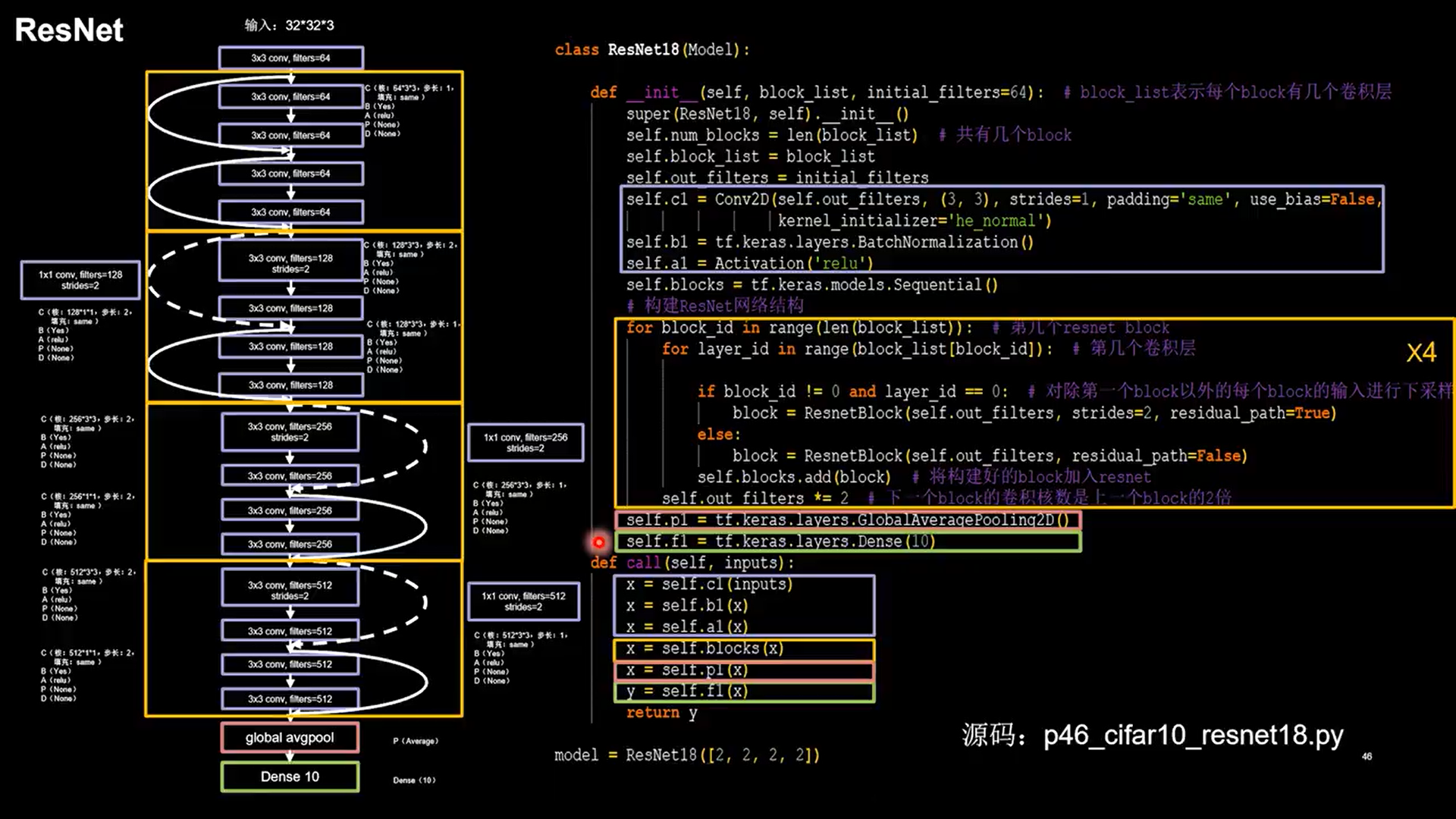
1 | class ResnetBlock(Model): |
25 循环神经网络 RNN
25.1 循环核


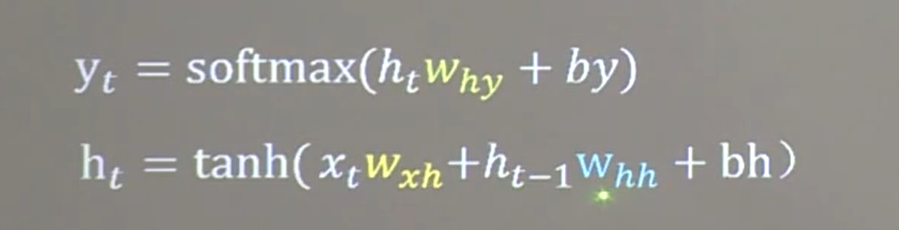
25.2 循环核时间步展开
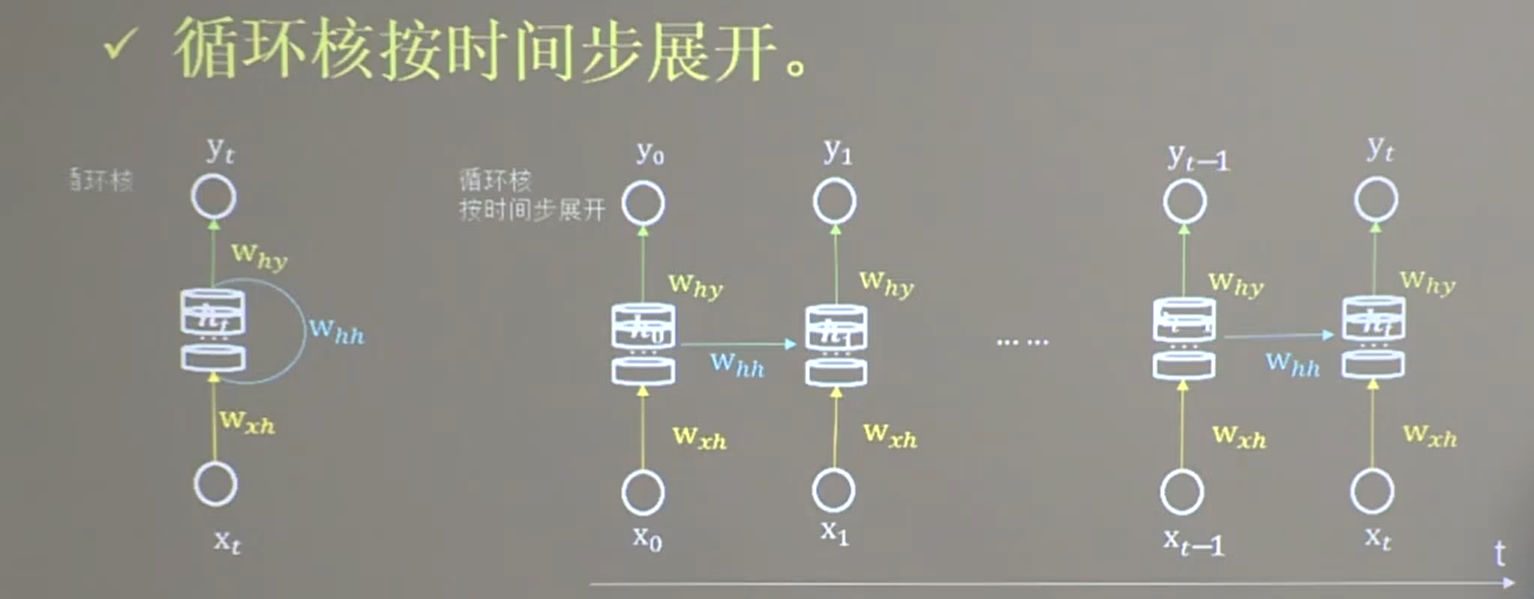

25.3 循环计算层
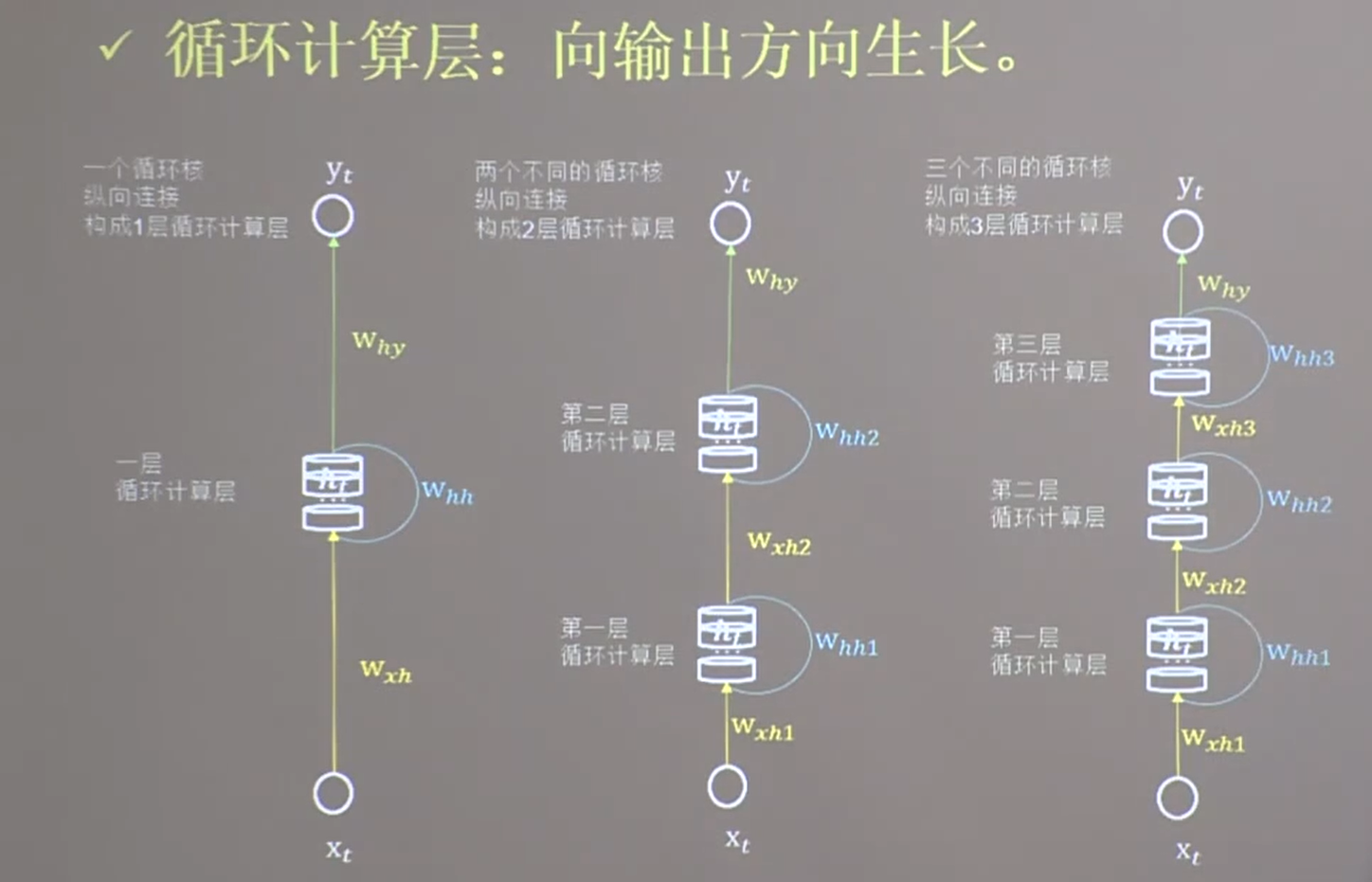
25.4 TF描述计算层

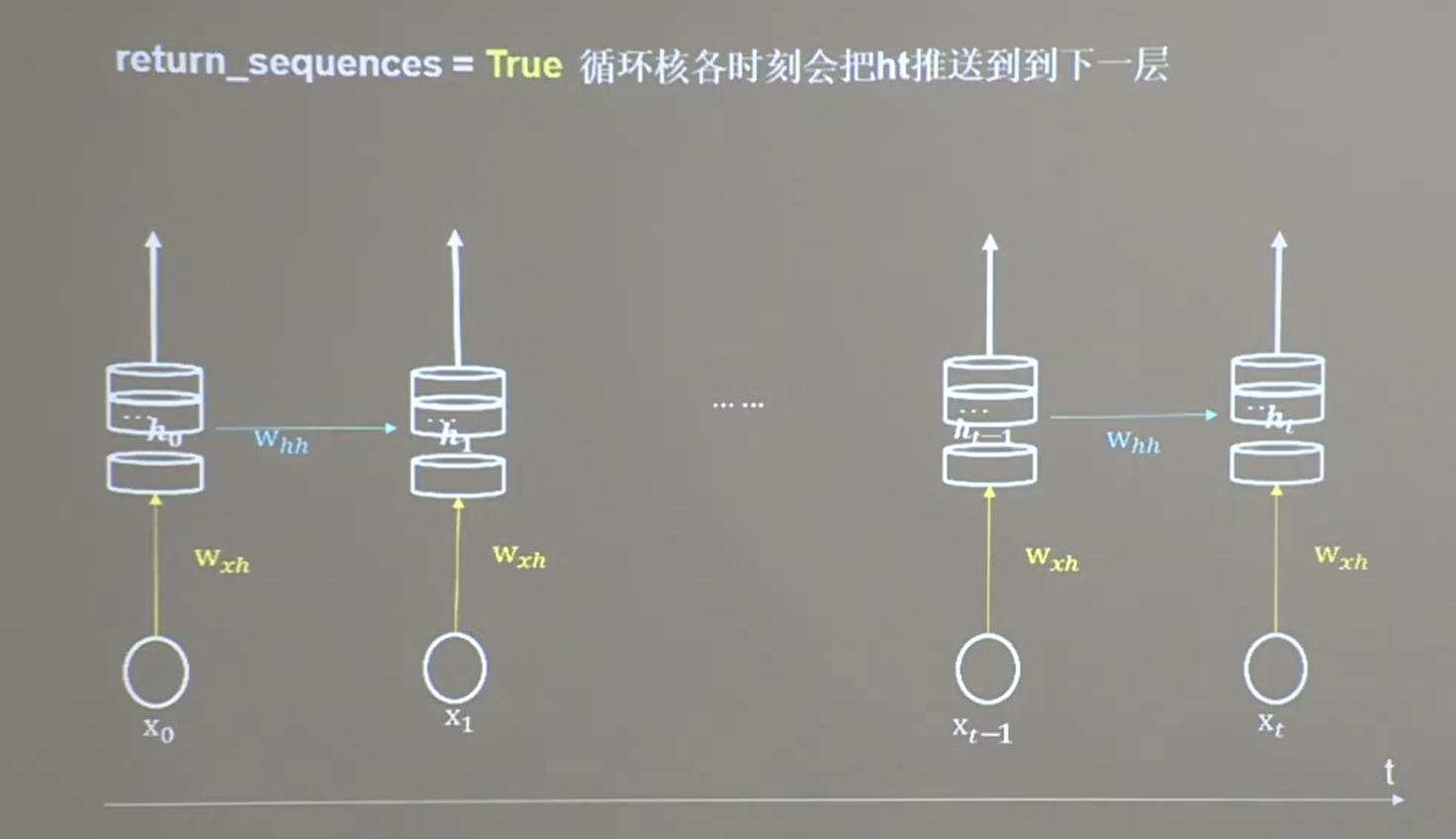
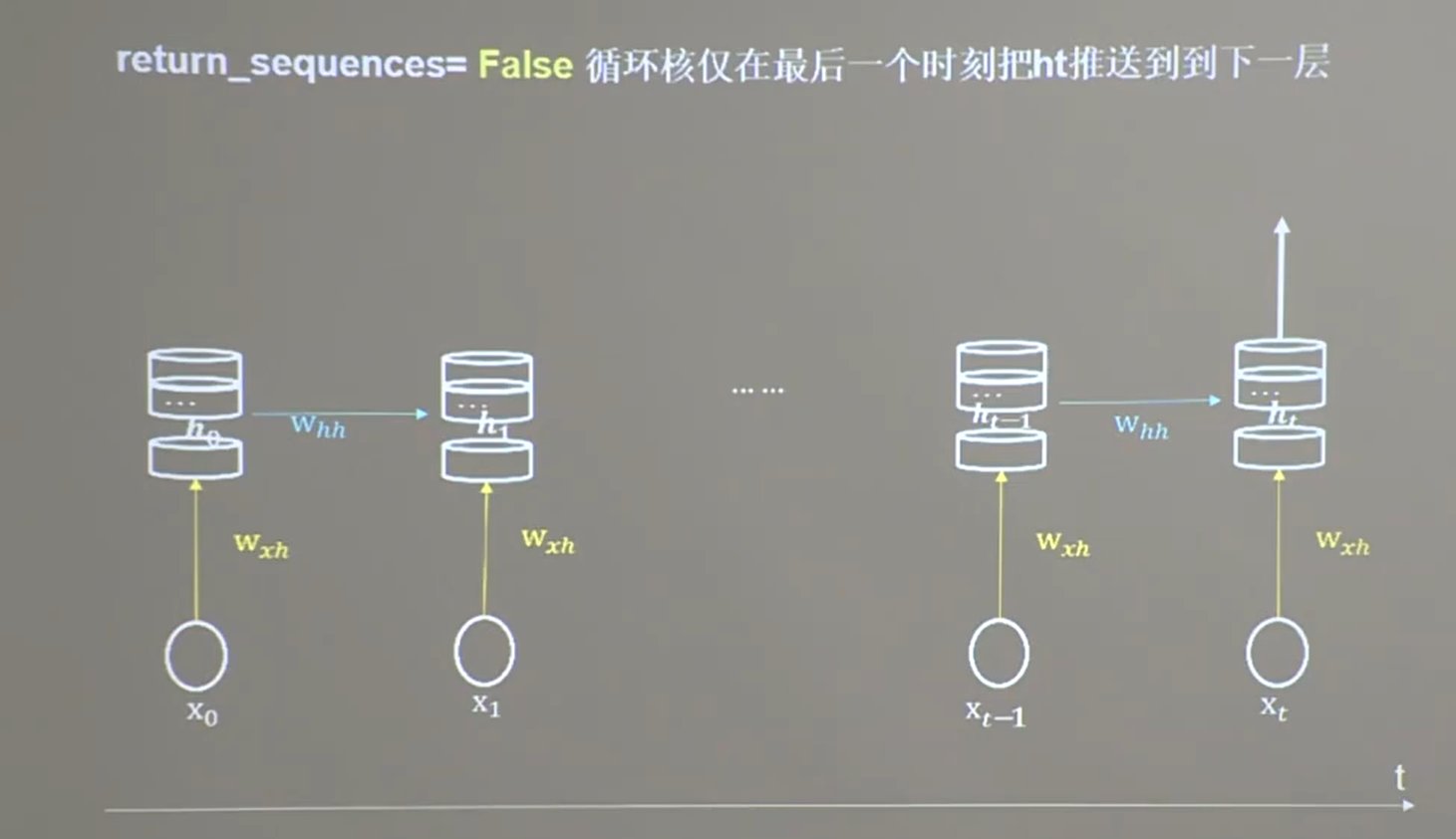
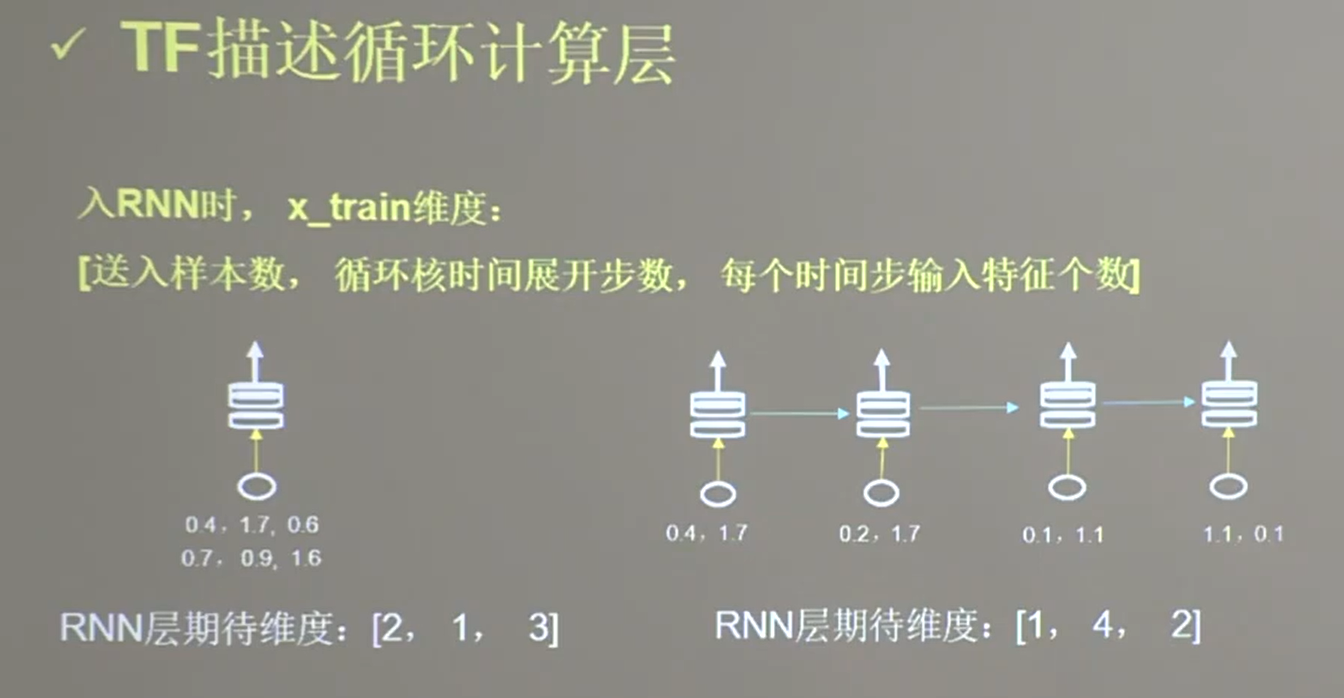
25.5 循环计算过程


26 Embedding编码
